分解机模型简介及其推导（Factorization Machine）

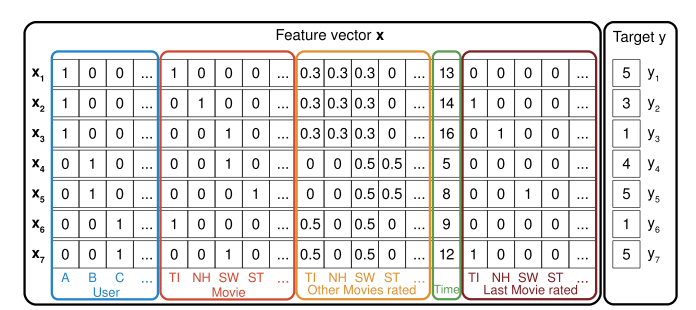
假设有一个预测问题，其数据是一个矩阵$X \in R^{n\times p}$。其中，$X$的第$i$行是$x_i \in R^p$，用一个$p$维的向量描述一个对象，而$y_i$则表示第i行数据对应的标签（如图1所示）。分解机是将输入变量编程一个$d$阶相互交互的参数。例如，

假设分解机分解成2阶的结果是：

\tilde{y}(x):= w_0 + \sum_{j=1}^p w_jx_j + \sum_{j=1}^{p}\sum_{j'=j+1}^{p}x_jx_{j'}\sum_{f=1}^kv_{j,f}v_{j'f}

其中，$k$是分解的维度，模型的参数集合是

\Theta=\{w_0,w_1,\cdots,w_p,v_{1,1},\cdots,v_{p,k}\}