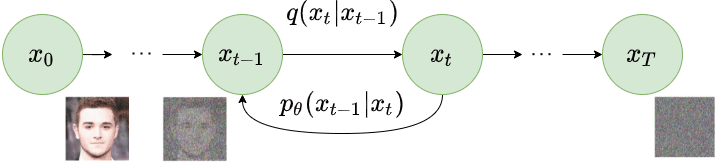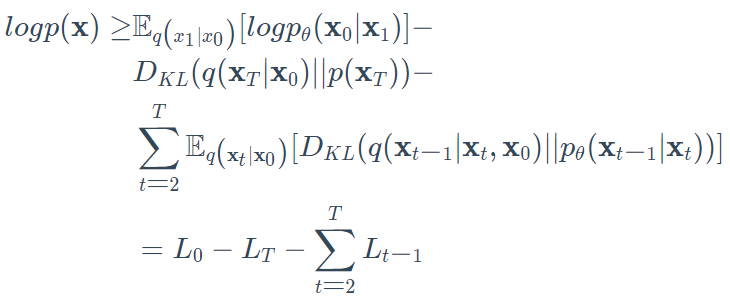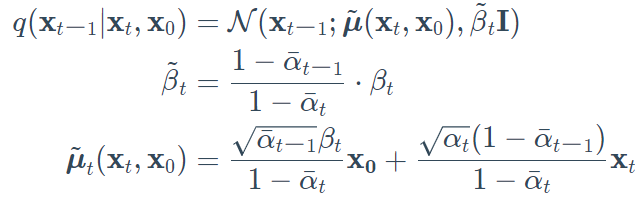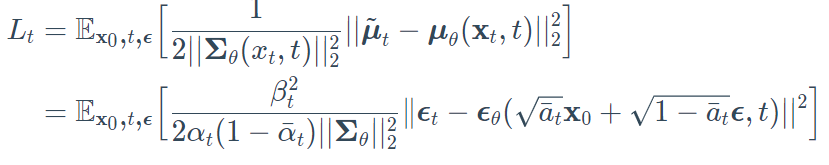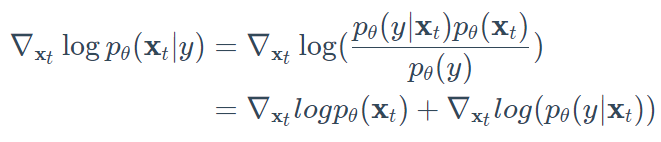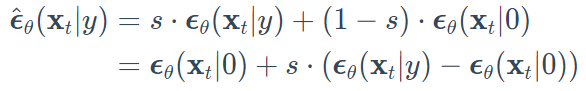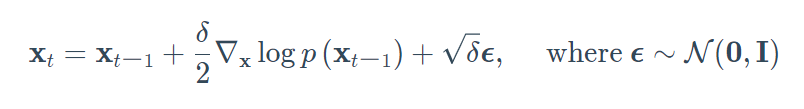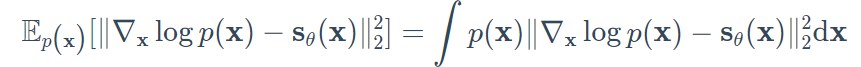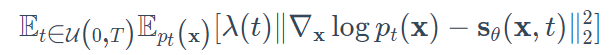扩散模型是如何工作的：从0开始的数学原理——How diffusion models work: the math from scratch

随着DALL·E2的发布，大家发现Text-to-Image居然可以取得如此好的效果。也让diffusion模型变得非常受欢迎。开源的Stable Diffusion的发布，更让这种研究被推向火热。但是，作为生成对抗网络（GAN）的继任新秀，扩散模型虽然火热，但是背后的数学原理可能很多人也不太了解。因此，AI Summer的工作人员Sergios Karagiannakos,Nikolas Adaloglou几人发布了一篇从0开始讲解Diffusion Model背后的数学推导，全文很长，但是数学知识用到的并不那么高深，了解基本的统计和贝叶斯公式即可理解整个扩散模型。

这篇博客不仅介绍了扩散模型背后的数学原理，也讲述了如何训练扩散模型以及提高扩散模型训练效率的种种技巧，十分值得大家钻研。

本文翻译自他们的博客：[How diffusion models work: the math from scratch](https://theaisummer.com/diffusion-models/ "How diffusion models work: the math from scratch")。欢迎想要理解diffusion model背后原理和研究相关模型的童鞋阅读。如有问题，也欢迎指出（官方邮箱地址datalearner at aliyun.com）。

[TOC]

#### 简介
扩散模型是一类新的最先进的生成模型，可以生成多样化的高分辨率图像。在OpenAI、Nvidia和Google成功地训练了大规模的模型之后，它们已经吸引了很多人的注意。基于扩散模型的实例架构有GLIDE、DALLE-2、Imagen和完全开源的稳定扩散。

但是它们背后的主要原理是什么呢？

在这篇博文中，我们将从基本原理开始挖掘。目前已经有一堆不同的基于扩散的架构。我们将重点讨论最突出的一个，即由Sohl-Dickstein等人最初提出的去噪扩散概率模型（DDPM），然后由Ho.等人在2020年提出。其他各种方法将在较小范围内讨论，如稳定扩散和基于分数的模型。

> 扩散模型与之前所有的生成方法有着本质的区别。直观地说，它们旨在将图像生成过程（采样）分解为许多小的 "去噪 "步骤。

这背后的直觉是，模型可以在这些小的步骤中修正自己，逐渐产生一个好的样本。在某种程度上，这种完善表征的想法已经在αfold等模型中得到了应用。但是，嘿，没有什么是零成本的。这种迭代过程使得它们的采样速度很慢，至少与GANs相比是如此。

#### 扩散过程
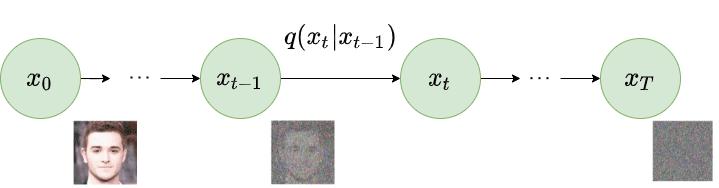
扩散模型的基本思想是相当简单的。他们把输入图像 $x\_0$并通过一系列的$T$步骤逐渐向其添加高斯噪声。我们将此称为正向过程。值得注意的是，这与神经网络的前向传递无关。如果你愿意，这部分对于为我们的神经网络生成目标（应用$t \lt T$噪声步骤后的图像）是必要的。

之后，神经网络被训练为通过逆转噪声过程来恢复原始数据。通过能够对反向过程进行建模，我们可以生成新的数据。这就是所谓的反向扩散过程，或者一般来说，生成式模型的采样过程。

怎么做？让我们深入研究一下数学，让它变得非常清晰。

#### 前向扩散
扩散模型可以被看作是潜变量模型。潜伏意味着我们指的是一个隐藏的连续特征空间。以这种方式，它们可能看起来类似于变异自动编码器（VAEs）。

在实践中，它们是用一个马尔科夫链的$T$步骤来制定的。这里，马尔可夫链意味着每一步只取决于前一步，这是一个温和的假设。重要的是，我们不受限制地使用特定类型的神经网络，与基于流量的模型不同。

给定一个数据点$x\_0$，从真实数据分布$q(x)(x\_0 \sim q(x))$中采样，我们可以通过添加噪声来定义一个前向扩散过程。具体来说，在马尔科夫链的每一步，我们添加方差为$\beta\_t$到$x\_{t-1}$的高斯噪声，产生一个新的潜在变量 $x\_{t}$，其分布为$q(x\_t|x\_{t-1})$。这个扩散过程可以表述如下：

```math
q(x_t|x_{t-1}) = \mathcal{N}(x_t;\mu_t=\sqrt{1-\beta_t}x_{t-1},\sum_t=\beta_tI)
```

<center>![](https://www.datalearner.com/resources/blog_images/2cead91f-a3e9-4269-ad94-d3eaa40e381c.png)</center>
<center></center>

由于我们处于多维情况下，$I$是身份矩阵，表明每个维度有相同的标准偏差$\beta\_t$。注意到，$q(x\_t|x\_{t-1})$是一个正态分布，其均值是$\mu\_t=\sqrt{1-\beta\_t}x\_{t-1}$，方差为$\sum\_t=\beta\_tI$，其中$\sum$是一个对角矩阵的方差（这里就是$\beta\_t$）。

因此，我们可以以一种可操作的方式来近似输入，数学上，这种后验概率如下：

```math
q(x_{1:T}|x_0) = \prod_{t=1}^{T}q(x_t|x_{t-1})
```

这里的$q(x\_{1:T})$意味着我们从时间1到$T$重复的应用$q$。这也称为trajectory。

到目前为止，这么好？好吧，不! 对于时间步长t=500，我们需要应用q 500次，以便对$x\_t$进行采样，难道我们真的不能做得更好吗？

重参数化对此提供了一个神奇的补救办法。

#### 重新参数化的技巧：在任何时间步长的可操作的闭式采样

如果我们定义$\alpha\_t=1-\beta\_t,\overline{\alpha}\_t=\prod\_{s=0}^t\alpha\_s$，其中$\epsilon\_0,\cdots,\epsilon\_{t-2},\epsilon\_{t-1}\sim \mathcal{N}(0,I)$，那么，我们可以使用重新参数化的技巧证明如下：

```math
\begin{aligned}
   x_t&=\sqrt{1-\beta_t}x_{t-1} + \sqrt{\beta_t}\epsilon_{t-1} \\
   &\\
  &=\sqrt{\alpha}x_{t-2} + \sqrt{1-\alpha_t}\epsilon_{t-2} \\
  &\\
  &=\cdots \\
  &\\
  &=\sqrt(\overline{\alpha}_t)x_0+\sqrt{1-\overline{\alpha}_t}\epsilon_0
\end{aligned}
```

> 注意：由于所有时间段都有相同的高斯噪声，我们从现在开始只使用符号$\epsilon$。

因此，为了产生一个样本，我们可以使用如下公式：
```math
x_t\sim q(x_t|x_0)=\mathcal{N}(x_t;\sqrt{\overline{\alpha}_t}x_0,(1-\overline{\alpha_t}I)
```

由于$\beta\_t$是一个超参数，我们可以预先计算所有时间步长的$\alpha\_t$和$\overline{\alpha}\_t$。这意味着我们在任何一个时间点t对噪声进行采样，并一次性得到$x\_t$。因此，我们可以在任何一个任意的时间段对我们的潜变量x进行采样。这将是我们以后计算可操作的目标损失$L\_t$的目标。

#### 方差Schedule
方差参数$\beta\_t$可以固定为一个常数，也可以选择作为T时间段的一个时间表。事实上，人们可以定义一个方差表，它可以是线性的、二次的、余弦的等等。最初的DDPM作者利用了一个从$\beta\_1=10^{-4}$到$\beta\_T=0.02$增加的线性时间表。Nichol等人2021年的研究表明，采用余弦时间表效果更好。

<center>![](https://www.datalearner.com/resources/blog_images/f01d5859-bf40-44d4-9abe-ba0f0952edbc.png)</center>
<center></center>

#### 反向扩散
当$T \to \infty$时，潜在的$x\_T$几乎是一个各向同性的高斯分布。因此，如果我们设法学习反向分布$q(x\_{t-1}|x\_t)$，我们可以对$x\_T$进行采样，从$\mathcal{N}(0,I)$中获取样本，运行反向过程并从$q(x\_0)$，从原始数据分布中产生一个新的数据点。

问题是我们如何对反向扩散过程进行建模。

#### 用神经网络逼近反向过程
在实际情况中，我们不知道$q(x\_{t-1}|x\_{t})$，由于估计$q(x\_{t-1}|x\_{t})$需要涉及数据分布的计算，所以这是难以解决的。

相反，我们用一个参数化的模型$p\_\theta$（例如一个神经网络）来近似$q(x\_{t-1}|x\_{t})$。由于$q(x\_{t-1}|x\_{t})$也将是高斯的，对于足够小的$\beta\_t$，我们可以选择是高斯的，只需对平均值和方差进行参数化：

```math
p_{\theta}(x_{t-1}|x_t)=\mathcal{N}(x_{t-1};\mu_\theta(x_t,t),\sum_\theta(x_t,t))
```

<center>![](https://www.datalearner.com/resources/blog_images/0c2cf2af-4861-4c07-a1f0-d5424dad0f0d.png)</center>
<center></center>

如果我们对所有的时间步数应用反向公式（$p\_\theta(x\_{0:T})$也叫轨迹），我们可以从$x\_T$到数据分布：

```math
p_\theta(x_{0:T})=p_\theta(x_T)\prod_{t=1}^Tp_\theta(x_{t-1}|x_t)
```
通过对时间段t的额外调节，该模型将学会预测每个时间段的高斯参数（指平均值$\mu\_\theta(x\_t,t)$和协方差矩阵$\sum\_\theta(x\_t,t)$）。

但我们如何训练这样一个模型呢？

#### 训练一个扩散模型
如果我们退一步讲，我们可以注意到，qq和pp的组合与变异自动编码器（VAE）非常相似。因此，我们可以通过优化训练数据的负对数似然来训练它。经过一系列的计算（我们在此不做分析），我们可以把证据下限（ELBO）写成如下：

<center>![](https://www.datalearner.com/resources/blog_images/7a357565-88eb-4f98-bbad-69a4968fdef2.png)</center>
<center></center>

我们来分析一下这些内容：

1、$E\_{q(x\_1|x\_0)}[logp\_\theta(\bold{x\_0}|\bold{x\_1})]$可以当作是一个重建项（a reconstruction term），类似于变量自动编码器ELBO中的一个。在Ho等人的研究中，这个术语是用一个单独的解码器学习的。

2、$D\_{KL}(q(\bold{x}\_T|\bold{x}\_0)||p(\bold{x}\_T))$显示了$\bold{x}\_T$与标准高斯是多么的相似。注意到，整个项都没有可训练的参数，因此，训练过程这个项会被忽略。

3、最后的第三项$\sum\_{t=2}^TL\_{t-1}$也表示为$L\_t$，描述了期望的去噪步骤$p\_\theta(\bold{x\_{t-1}}|\bold{x}\_t)$与近似项$q(\bold{x\_{t-1}}|\bold{x}\_t,\bold{x}\_0)$之间的差异。

很明显，通过ELBO，最大化的可能性可以归结为学习去噪步骤$L\_t$。

> 重要提示：尽管$q(\bold{x\_{t-1}}|\bold{x}\_t)$是难以解决的，但Sohl-Dickstein等人说明，通过对$\bold{x}\_0$的附加条件，可以使它变得容易解决。

直观地说，画家（我们的生成模型）需要一个参考图像（$\bold{x}\_0$）来慢慢绘制（反向扩散步骤$q(\bold{x\_{t-1}}|\bold{x}\_t,\bold{x}\_0)$）一个图像。因此，当且仅当我们有$\bold{x}\_0$作为参考时，我们可以向后退一小步，即从噪声中生成一个图像。

换句话说，我们可以在噪声水平t的条件下对$\bold{x}\_t$进行采样。由于$\alpha\_t=1-\beta\_t$和$\overline\alpha\_t=\prod\_{s=0}^t$，我们可以证明：

<center>![](https://www.datalearner.com/resources/blog_images/0ca94afe-c180-44eb-babf-4d34f9b13303.png)</center>
<center></center>

> 请注意，$\alpha\_t$和$\overline\alpha\_t$只取决于$\beta\_t$，所以它们可以被预先计算出来。

这个小技巧为我们提供了一个完全可操作的ELBO。上述属性还有一个重要的副作用，正如我们在重参数化技巧中已经看到的，我们可以将$\bold{x}\_0$表示为：

```math
\bold{x}_0 = \frac{1}{\sqrt{\overline\alpha_t}}(\bold{x}_t-\sqrt{1-\overline{\alpha}_t\bold{\epsilon}})
```

这里的$\epsilon \sim \mathcal{N}(0,I)$。

通过合并最后两个方程，现在每个时间步长将有一个平均数$\tilde{\mu}\_t$（我们的目标），它只取决于$\bold{x}\_t$：

```math
\tilde{\mu}_t(x_t)=\frac{1}{\sqrt{\alpha_t}}(x_t - \frac{\beta_t}{\sqrt{1-\overline{\alpha}_t}}\epsilon)
```

因此，我们可以使用一个神经网路$\epsilon\_\theta(\bold{x}\_t,t)$来近似$\epsilon$并得到如下均值结果：

```math
\tilde{\mu}_\theta(x_t,t)=\frac{1}{\sqrt{\alpha_t}}(x_t - \frac{\beta_t}{\sqrt{1-\overline{\alpha}_t}}\epsilon_\theta(x_t,t))
```

因此，损失函数（ELBO中的去噪项）可以表示为：

<center>![](https://www.datalearner.com/resources/blog_images/e189b3e1-cd4d-4cb6-9e62-ff53bde061f7.png)</center>
<center></center>

这有效地告诉我们，该模型不是预测分布的平均值，而是预测每个时间点t的噪声ϵ。

Ho et.al 2020对实际损失项做了一些简化，因为他们忽略了一个加权项。简化后的版本优于完整的目标：

```math
L_t^{\text{simple}} = E_{x0,t,\epsilon}[||\bold{\epsilon}-\bold{\epsilon}_0(\sqrt{\overline{\alpha}_t}\bold{x}_0 + \sqrt{1-\overline{\alpha}_t}\bold{\epsilon},t)||^2]
```

作者发现，优化上述目标比优化原始ELBO效果更好。这两个方程的证明可以在Lillian Weng的[这篇优秀文章](https://lilianweng.github.io/posts/2021-07-11-diffusion-models/#reverse-diffusion-process "这篇优秀文章")或[Luo等人2022年的文章](https://arxiv.org/abs/2208.11970 "Luo等人2022年的文章")中找到。

此外，Ho等人2020年决定保持方差固定，让网络只学习平均值。后来Nichol等人2021年对此进行了改进，他们决定让网络学习协方差矩阵（$\sum$）简单，取得了更好的结果。

<center>![](https://www.datalearner.com/resources/blog_images/845796bb-47b5-493b-bb28-e4088c27a448.png)</center>
<center></center>

#### 架构
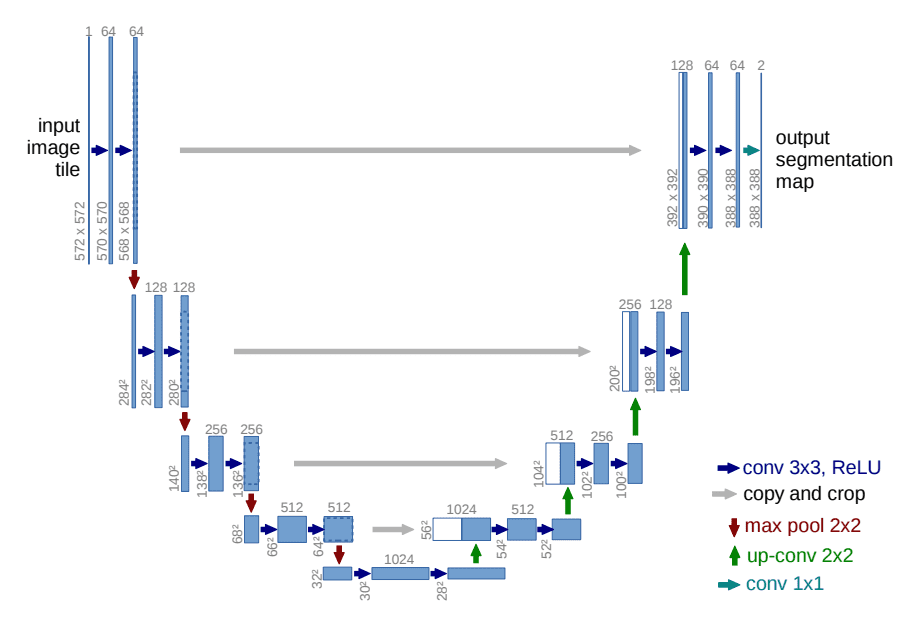
到目前为止，我们还没有提到的一件事是模型的架构是什么样子的。请注意，模型的输入和输出应该是相同大小的。

为此，Ho等人采用了一个U型网。如果你对U-Net不熟悉，请随时查看我们过去关于主要U-Net架构的文章。简而言之，U-Net是一种对称的架构，其输入和输出的空间大小相同，在相应特征维度的编码器和解码器块之间使用跳过连接。通常情况下，输入图像首先被降频，然后被升频，直到达到其初始尺寸。

在DDPMs的原始实现中，U-Net由[Wide ResNet块](https://theaisummer.com/skip-connections/#resnet-skip-connections-via-addition "Wide ResNet块")、[分组归一化](https://theaisummer.com/normalization/#group-normalization-2018 "分组归一化")以及[自我注意块](https://theaisummer.com/attention/ "自我注意块")组成。

扩散时间段t是通过在每个残差块中加入一个[正弦位置嵌入](https://theaisummer.com/positional-embeddings/ "正弦位置嵌入")来指定的。欲了解更多细节，请随时访问[官方GitHub仓库](https://github.com/hojonathanho/diffusion "官方GitHub仓库")。关于扩散模型的详细实现，请[查看Hugging Face的这篇精彩文章](https://huggingface.co/blog/annotated-diffusion "查看Hugging Face的这篇精彩文章")。

<center>![](https://www.datalearner.com/resources/blog_images/bfa88da3-cd04-4f6d-a8c8-16d2d4ca19c5.png)</center>
<center></center>

#### 条件性图像生成：引导扩散
图像生成的一个关键方面是调节采样过程，以操纵生成的样本。在这里，这也被称为引导性扩散。

甚至有一些方法将图像嵌入到扩散中，以便 "引导 "生成。从数学上讲，引导指的是用一个条件y，即类别标签或图像/文本嵌入来调节先验数据分布p(x)，导致$p(x|y)$。

为了把扩散模型$p\_\theta$变成一个条件扩散模型，我们可以在每个扩散步骤中加入条件信息y:

```math
p_\theta(\bold{x}_{0:T}|y) = p_\theta(\bold{x}_T)\prod_{t=1}^Tp_\theta(\bold{x}_{t-1}|\bold{x}_t,y)
```

在每个时间点都能看到调节的事实，这可能是文字提示的优秀样本的一个很好的理由。

一般来说，引导扩散模型的目的是学习$\nabla\log p\_\theta(\bold{x}\_t|y)$，所以使用贝叶斯规则，我们可以写出：

<center>![](https://www.datalearner.com/resources/blog_images/ffd6fe5f-564f-49a0-b2c8-3d1ef287e68e.png)</center>
<center></center>

因为梯度算子$\nabla\_{x\_t}$只代表$\bold{x}\_t$，$p\_\theta(y)$被移除，所以y没有梯度。此外，请记住，$log(ab)=log(a)+log(b)$。

再加上一个指导性的标量项s，我们就有：

```math
\nabla\log p_\theta(\bold{x}_t|y) = \nabla\log p_\theta(\bold{x}_t) + s \cdot \nabla \log (p_\theta(y|\bold{x}_t))
```

利用这一表述，让我们对分类器和无分类器的引导进行区分。接下来，我们将介绍两个旨在注入标签信息的方法系列。

#### 分类指导

Sohl-Dickstein等人以及后来的Dhariwal和Nichol表明，我们可以使用第二个模型，即分类器$f\_\phi(y|\bold{x}\_t,t)$，在训练过程中引导向目标类y的扩散。为了达到这个目的，我们可以在噪声图像$\bold{x}\_t$上训练一个分类器$f\_\phi(y|\bold{x}\_t,t)$，以预测其类别y。然后我们可以使用梯度$\nabla f\_\phi(y|\bold{x}\_t)$来引导扩散，怎么做？

我们可以建立一个具有均值$\mu\_\theta(x\_t,t)$和方差$\sum\_{\theta}(\bold{x}\_t|y)$的类条件扩散模型。

由于$p\_\theta \sim \mathcal{N}(\mu\_\theta,\sum\_{\theta})$，我们可以用上一节的引导公式表明，均值被y类的$\log f\_\phi(y|\bold{x}\_t)$的梯度所扰动，结果是：

```math
\hat{\mu}(\bold{x}_t|y) = \mu_\theta(\bold{x}_t|y) + s\cdot \sum_\theta(\bold{x}_t|y) \nabla_{x_t}\log f_\phi(y|\bold{x}_t,t)
```

在Nichol等人著名的GLIDE论文中，作者扩展了这个想法，并使用CLIP嵌入来指导扩散。Saharia等人提出的CLIP由一个图像编码器g和一个文本编码器h组成。它分别产生一个图像和文本嵌入$g(\bold{x}\_t)$和$h(c)$，其中c是文本标题。

因此，我们可以用它们的点积来扰动梯度：

```math
\hat{\mu}(\bold{x}_t|c) = \mu_(\bold{x}_t|c) + s\cdot \sum_\theta(\bold{x}_t|c) \nabla_{x_t}g(x_t)\cdot h(c)
```

因此，他们设法将生成过程 "引向 "用户定义的文本标题。

<center>![](https://www.datalearner.com/resources/blog_images/7777ca5f-4f1d-4aae-9ce5-6b6b53d30e1b.png)</center>
<center></center>

#### 无分类指导

使用与之前相同的表述，我们可以将无分类器的引导扩散模型定义为：
```math
\nabla\log p_\theta(\bold{x}_t|y) = s\cdot\nabla\log p(\bold{x}_t|y) + (1-s)\cdot \nabla \log p(\bold{x}_t)
```

正如Ho & Salimans所提议的那样，不需要第二个分类器模型就可以实现指导作用。事实上，他们使用的是完全相同的神经网络，而不是训练一个单独的分类器，作者将条件性扩散模型$\epsilon\_\theta(\bold{x}\_t|y)$与无条件性模型$\epsilon\_\theta(\bold{x}\_t|0)$一起训练。在训练过程中，他们随机地将类y设置为0，这样模型就同时接触到了有条件和无条件的设置：

<center>![](https://www.datalearner.com/resources/blog_images/0f9c1fa9-2412-4332-a633-4770df1dfc5c.png)</center>
<center></center>

> 请注意，这也可以用来 "注入 "文本嵌入，正如我们在分类器指导中显示的那样。

这个公认的 "怪异 "过程有两个主要优点。

- 它只使用一个单一的模型来指导扩散。

- 当对难以用分类器预测的信息（如文本嵌入）进行调节时，它简化了指导。

Saharia等人提出的Imagen在很大程度上依赖于无分类器的引导，因为他们发现这是产生具有强大图像-文本排列的样本的一个关键因素。关于Imagen方法的更多信息，请看AI Coffee Break与Letitia的这段视频。

<center>https://youtu.be/xqDeAz0U-R4</center>
<center></center>

#### 扩大扩散模型的规模
你可能会问这些模型的问题是什么。好吧，将这些U型网扩展到高分辨率的图像中，在计算上是非常昂贵的。这给我们带来了两种将扩散模型扩展到高分辨率的方法：级联扩散模型和潜伏扩散模型。

##### 级联扩散模型
Ho等人在2021年引入了级联扩散模型，以努力产生高保真的图像。级联扩散模型包括一个由许多连续扩散模型组成的管道，生成分辨率越来越高的图像。每个模型通过连续地对图像进行上采样并增加更高分辨率的细节，生成一个比前一个质量更好的样本。为了生成一个图像，我们从每个扩散模型中依次取样。

<center>![](https://www.datalearner.com/resources/blog_images/a3a33132-3c08-4c35-b009-04f685ed15c6.png)</center>
<center></center>

为了获得级联架构的良好效果，对每个超级分辨率模型的输入进行强有力的数据增强是至关重要的。为什么呢？因为它可以减轻之前级联模型的复合误差，以及由于训练-测试不匹配造成的误差。

研究发现，高斯模糊是实现高保真度的一个关键转变。他们把这种技术称为调节增强。

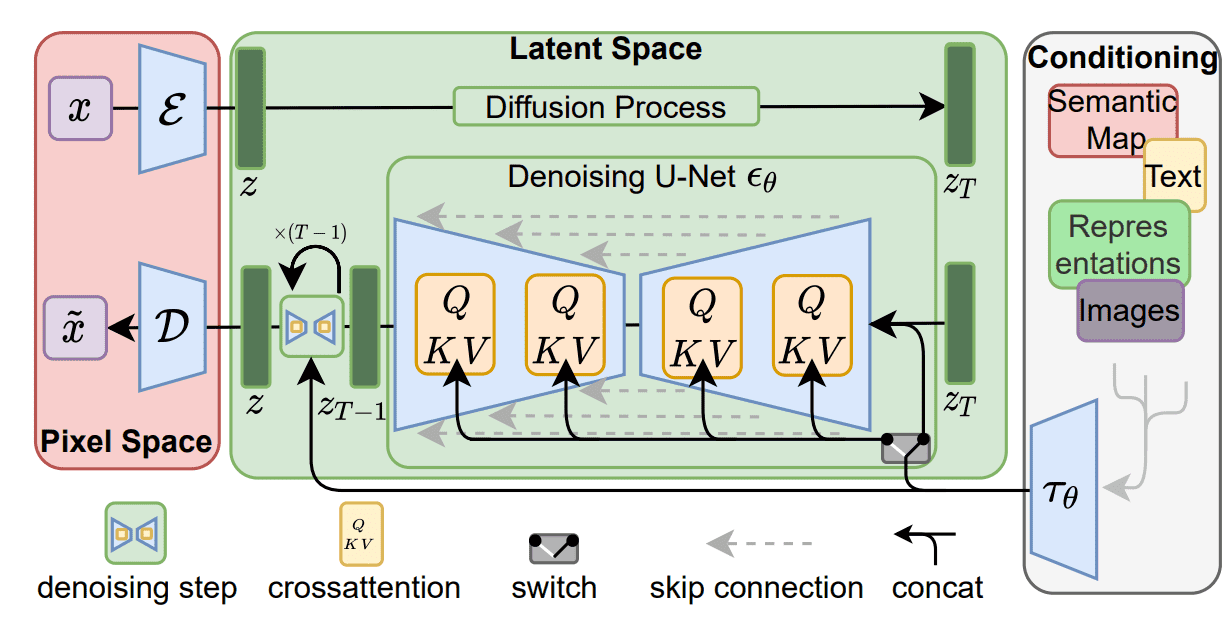
#### 稳定的扩散（Stable diffusion）：潜在扩散模型

潜在扩散模型是基于一个相当简单的想法：我们不是直接在高维输入上应用扩散过程，而是将输入投射到一个较小的潜伏空间，并在那里应用扩散。

更详细地说，Rombach等人建议使用编码器网络将输入编码为潜伏表示，即$\bold{z}\_t=g(\bold{x}\_t)$。这一决定背后的直觉是通过在低维空间处理输入来降低训练扩散模型的计算需求。之后，一个标准的扩散模型（U-Net）被应用于生成新的数据，这些数据被一个解码器网络放大。

如果一个典型的扩散模型（DM）的损失被表述为：

```math
L_{DM} = E_{x,t,\epsilon}[||\epsilon - \epsilon_\theta(\bold{x}_t,t)||^2]
```

然后，给定编码器$\xi$和一个潜在表示$z$，那么一个潜在扩散模型（LDM）的损失函数可以表示为：

```math
L_{DM} = E_{\xi(x),t,\epsilon}[||\epsilon - \epsilon_\theta(\bold{z}_t,t)||^2]
```

Stable Diffusion的模型：

<center>![](https://www.datalearner.com/resources/blog_images/4753ca81-0a45-43c8-86af-17881a235c29.png)</center>
<center></center>

欲了解更多信息，请看这个视频：
https://youtu.be/ltLNYA3lWAQ

#### 基于分数的生成模型
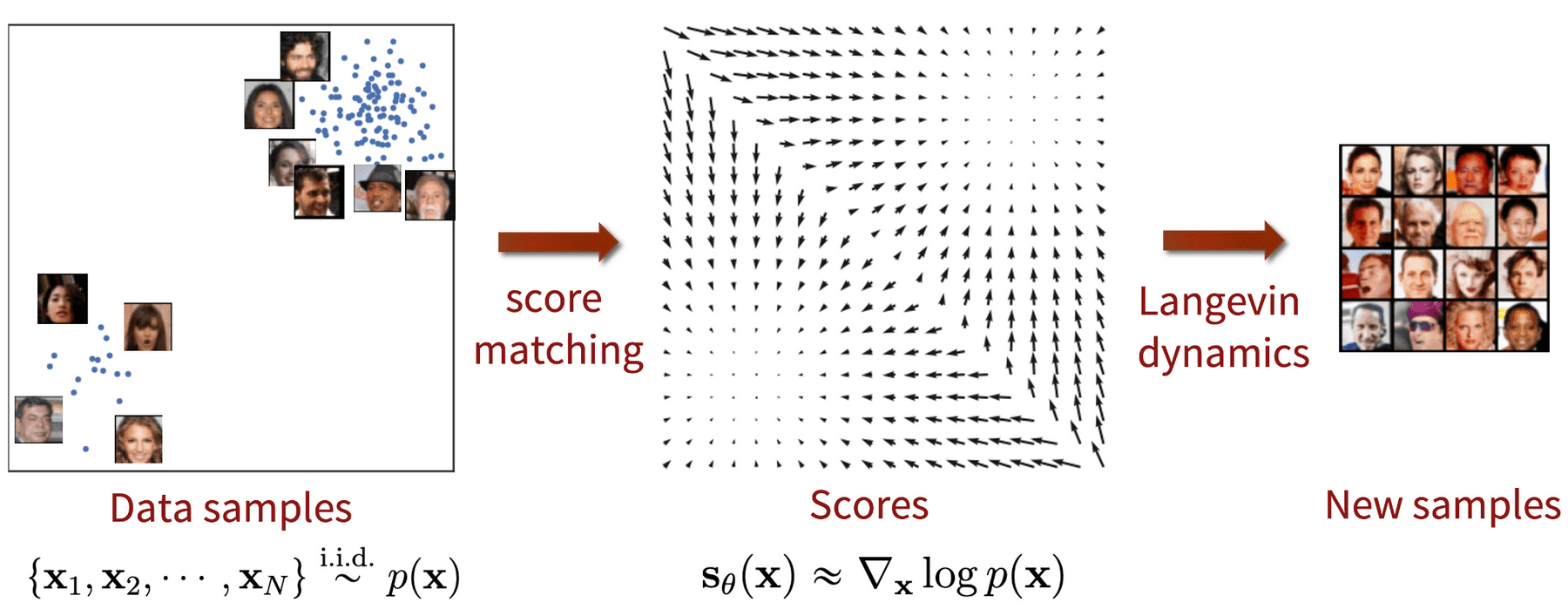
在DDPM论文发表的同时，Song和Ermon提出了一种不同类型的生成模型，似乎与扩散模型有许多相似之处。基于分数的模型利用分数匹配和Langevin动力学来解决生成式学习。

> 分数匹配指的是对数概率密度函数梯度的建模过程，也被称为分数函数。郎咸平动力学是一个迭代过程，可以从一个分布中只使用其分数函数来抽取样本。

<center>![](https://www.datalearner.com/resources/blog_images/f090aa96-29ac-468d-8872-3bc47cf6deef.png)</center>
<center></center>

其中$\delta$是步长大小。

假设我们有一个概率密度$p(x)$，并且我们定义分数函数为$\nabla\_x\log p(x)$ 。然后我们可以训练一个神经网络$s\_{\theta}$来估计 $\nabla_x \log p(x)$，而不用先估计$p(x)$。训练目标可以表述如下：

<center>![](https://www.datalearner.com/resources/blog_images/e2cfe5d1-75b9-4e6b-8b21-eefff4b24d71.png)</center>
<center></center>

然后通过使用Langevin动力学，我们可以使用近似的分数函数直接从p(x)中采样。

如果你错过了，引导式扩散模型使用这种基于分数的模型的表述，因为它们直接学习 $\nabla\_x \log p(x)$。当然，他们并不依赖朗文动力学。

##### 为基于分数的模型添加噪音：噪声条件得分网络(NCSN)
> 到目前为止的问题是：在低密度地区，估计的分数函数通常是不准确的，因为那里的数据点很少。因此，使用Langevin动力学采样的数据质量并不好。

他们的解决方案是对数据点进行噪声扰动，然后在噪声数据点上训练基于分数的模型。事实上，他们使用了多种规模的高斯噪声扰动。

因此，添加噪声是使DDPM和基于分数的模型都能工作的关键。

<center>![](https://www.datalearner.com/resources/blog_images/c17320bb-ea8b-41a5-99a9-abc990ae411a.png)</center>
<center></center>

在数学上，给定数据分布$p(x)$，我们用高斯噪声进行扰动$\mathcal{N}(\textbf{0}, \sigma_i^2 I)$ 其中$i=1,2,\cdots,L$得到一个噪声扰动的分布：

```math
p_{\sigma_i}(x)=\int p(y)\mathcal N(x;y,\sigma_i^2 I)d \bold{y}
```

然后我们训练一个网络$s\_\theta(\mathbf{x},i)$，称为基于噪声条件的评分网络（NCSN）来估计评分函数$\nabla\_\mathbf{x}\log d\_{\sigma_i}(\mathbf{x})$。训练目标是所有噪声尺度的Fisher分歧的加权和：

```math

\sum_{i=1}^L\lambda(i)E_{p\sigma_i(x)}[||\nabla_x\log p_{\sigma_i}(\bold{x})-s_\theta(\bold{x},i)||^2_2]

```

##### 通过随机微分方程（SDE）进行基于分数的生成性建模

Song等人在2021年探讨了基于分数的模型与扩散模型的联系。为了将NSCNs和DDPMs都囊括在同一伞下，他们提出了以下建议。

我们不使用有限数量的噪声分布来扰动数据，而是使用连续的分布，这些分布根据扩散过程随时间演变。这个过程由一个规定的随机微分方程（SDE）来模拟，它不依赖于数据，也没有可训练的参数。通过逆转这个过程，我们可以生成新的样本。

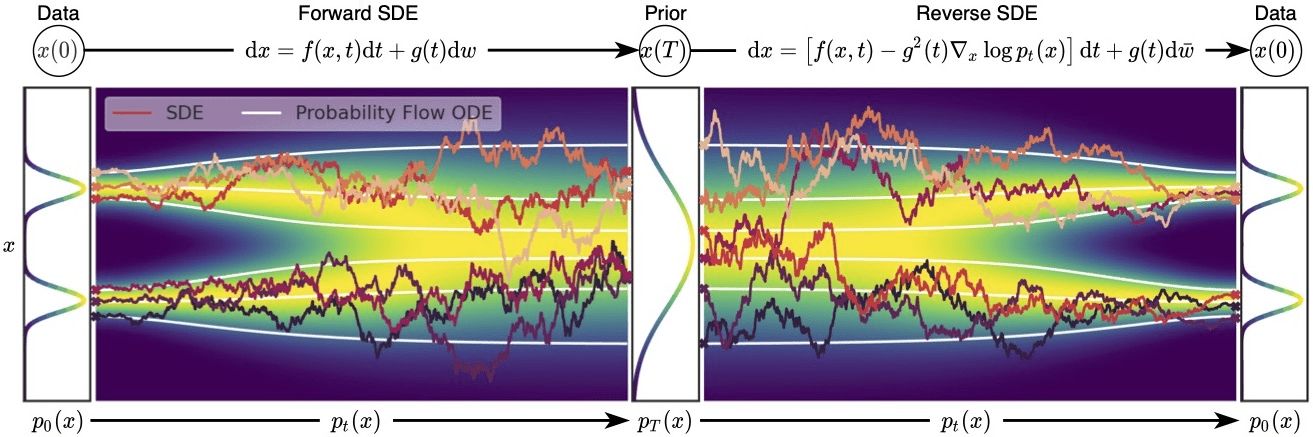
<center>![](https://www.datalearner.com/resources/blog_images/8ebaf761-fcaf-4377-a55a-1d6102fdd078.png)</center>
<center></center>

我们可以把扩散过程$\\{\mathbf{x}(t) \\}\_{t\in [0, T]}$定义为以下形式的SDE：

```math
d\bold{x} = \bold{f}(\bold{x},t)dt + g(t)d\bold{w}
```

其中，$\mathbf{w}$是维纳过程（又称布朗运动）。$\mathbf{f}(\cdot, t)$是一个矢量值函数，称为$\mathbf{x}(t)$的漂移系数，$g(\cdot)$是一个标度函数，称为$\mathbf{x}(t)$的扩散系数。请注意，SDE通常有一个唯一的强解。

> 为了理解我们为什么使用SDE，这里有一个提示：SDE的灵感来自于布朗运动，在布朗运动中，一些粒子在介质内随机移动。粒子运动的这种随机性模拟了数据上的连续噪声扰动。

在对原始数据分布进行足够长时间的扰动后，被扰动的分布会变得接近于一个可操作的噪声分布。

为了产生新的样本，我们需要逆转扩散过程。该SDE被选择为有一个相应的封闭形式的反向SDE:

```math
d\bold{x} = [\bold{f}(\bold{x},t)dt - g^2(t)\nabla_x \log p_t(\bold{x})]dt + g(t) d\bold{w}
```

为了计算反向SDE，我们需要估计分数函数$\nabla\_\mathbf{x}\log p\_t(\mathbf{x})$。这是用基于分数的模型$s\_\theta(\mathbf{x},i)$和Langevin动力学完成的。训练目标是Fisher分歧的连续组合：

<center>![](https://www.datalearner.com/resources/blog_images/f88238dd-5f90-4fec-9454-deac71cfee81.png)</center>
<center></center>

其中 $\mathcal{U}(0, T)$表示时间间隔上的均匀分布，$\lambda$是一个正的加权函数。一旦我们有了分数函数，我们就可以把它插入反向SDE并求解，以便从原始数据分布$p\_0(\mathbf{x})$中抽取$x(0)$。

> 有许多解决反向SDE的方案，我们在此不作分析。请务必查看原始论文或[作者的这篇优秀博文](https://yang-song.github.io/blog/2021/score/ "作者的这篇优秀博文")。

<center>![](https://www.datalearner.com/resources/blog_images/9804867a-c570-4be3-b88a-43f32edd98fc.png)</center>
<center></center>

#### 总结
让我们对这篇博文中所学到的主要内容做一个简单的总结。

- 扩散模型的工作原理是通过一系列的TT步骤将高斯噪声逐渐添加到原始图像中，这个过程被称为扩散。

- 为了对新数据进行采样，我们使用神经网络对反向扩散过程进行近似。

- 模型的训练是基于证据下限（ELBO）的最大化。

- 我们可以将扩散模型置于图像标签或文本嵌入的条件下，以便 "指导 "扩散过程。

- 级联扩散和潜伏扩散是两种将模型扩展到高分辨率的方法。

- 级联扩散模型是连续的扩散模型，可以生成分辨率越来越高的图像。

- 潜伏扩散模型（像稳定扩散）在较小的潜伏空间上应用扩散过程，以提高计算效率，使用变异自动编码器进行向上和向下取样。

- 基于分数的模型也将一连串的噪声扰动应用到原始图像上。但它们是用分数匹配和朗文动力学来训练的。尽管如此，它们最终的目标是相似的。

- 扩散过程可以被表述为一个SDE。解决反向SDE使我们能够生成新的样本。

- 最后，对于扩散模型和VAE或AE之间的更多联系，请查看这些非常好的博客。

扩散模型是如何工作的：从0开始的数学原理——How diffusion models work: the math from scratch

相关博客

最热博客