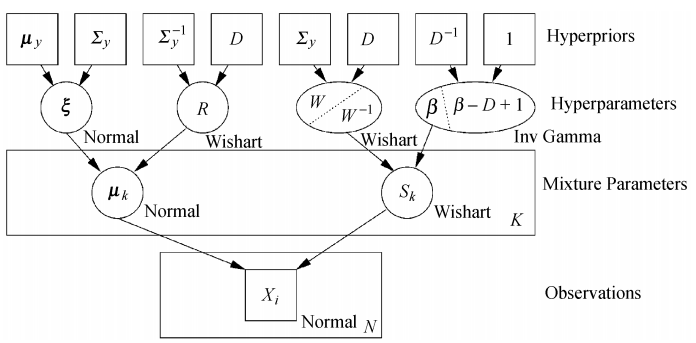
狄利克雷过程（Dirichlet Process Mixture Model，DPMM）的详细推导

2017/11/06 15:58:31

3,224 阅读

首先，我们从高斯混合模型开始。有K个类别的高斯混合模型可以写成如下形式：

p(x|\theta_1,\cdots,\theta_K)= \sum_{j=1}^K \pi_j \mathcal{N}(x|\mu_j,S_j)

参数集合$\theta_j = \{\mu_j,S_j,\pi_j\}$是第$j$个组件的参数。$\pi$是混合比例（正值，且总和为1），$\mu_j$是组件$j$的均值向量，$S_j$是精度（是逆协方差矩阵）。当我们对所有组件的参数定义一个联合先验分布$G_0$，且引入一个指示变量$c_i,i=1,\cdots,n$，那么上述模型可以写成如下形式：

\begin{aligned}

x_i|c_i,\Theta  & \sim \mathcal{N}(\mu_{c_i}, S_{c_i}) \\
&\\
c_i|\pi & \sim Dsicrete(\pi_1,.\cdots,\pi_K) \\
&\\
(\mu_j,S_j) & \sim G_0 \\
&\\
\pi|\alpha & \sim Dir(\alpha/K,\cdots,\alpha/K)

\end{aligned}

在给定了混合比例&\pi&的情况下，每个组件包含的观测值数量称之为占有数量，是一个多项式分布：

DataLearner 官方微信

欢迎关注 DataLearner 官方微信，获得最新 AI 技术推送

返回博客列表

p(n_1,\cdots,n_K | \pi)  = \frac{n!}{n_1!n_2!,\cdots,n_K!} \prod _{j=1}^K \pi_j^{n_j}

p(c_1,\cdots,c_n|\pi) = \prod_{j=1}^K\pi_j^{n_j}

p(c|\alpha) = \frac{\Gamma{(\alpha)}}{\Gamma(n+\alpha)} \prod_{j=1}^K \frac{ \Gamma(n_j+\alpha/K)}{\Gamma(\alpha/K)}

p(c_i=j|c_{-i},\alpha) = \frac{n_{-i,j} + \alpha/K }{n-1+\alpha}

p(c_i = j | c_{-i},\alpha) = \frac{ n_{-i,j}}{n-1+\alpha}

p(c_i = j | c_{-i},\alpha) = \frac{ \alpha }{n-1+\alpha}

(\mu_j|S_j,\xi, \rho) \sim \mathcal{N}( \xi, (\rho S_j)^{-1})

(S_j|\beta,W) \sim \mathcal{W}(\beta, (\beta W)^{-1})

(\mu_j,S_j) \sim \mathcal{NW}(\xi,\rho,\beta,\beta W)

p(\mu_j|\xi,R) \sim \mathcal{N}(\xi,R^{-1})

DataLearner 官方微信

热门博客