线性回归的目标是将一堆数据一分为二,如果数据是二维空间的点,那就找出一条直线将这些点一分为二,如果是三维空间的点,那就找出一个平面,如果是高维空间的点,那就找出一个超平面。这篇博客主要是描述线性回归的数学描述,主要是呈现线性回归相关的符号表示。提醒一点,在深度学习中,通常使用列向量表示一个数据,而在线性回归中,为了和大家保持一致,我们采用行向量表示一个数据点。
一、数据的表示
如下图,以二维空间的点为例,我们要找出一条直线:
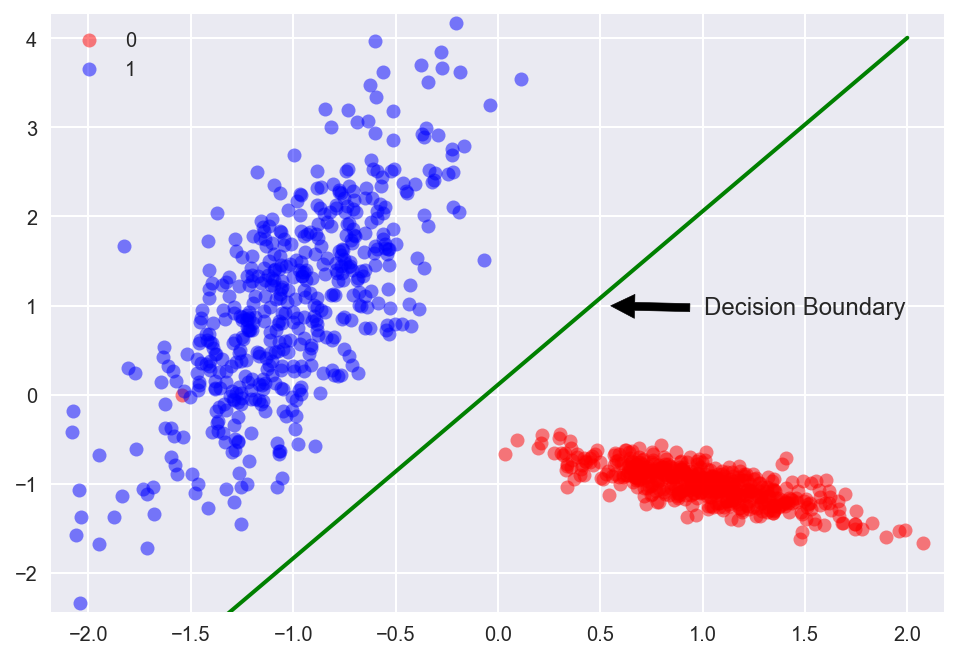
上述直线(决策边界)的形式就是:
```math
y = x\beta + \beta_0
```
扩展到高维,即每个数据点有$n$个维度,那么,其超平面的表示形式为:
欢迎关注 DataLearner 官方微信,获得最新 AI 技术推送
\begin{aligned}
y &= x_1\beta_1+\cdots+x_n\beta_n+\beta_0 \\
\\
& = \sum_{j=1}^n x_j\beta_j + \beta_0
\end{aligned}
对于一组$m$个数据,扩展到多维数据之后,假设我们有一组数据$\bold{X}=\{\bold{x_1},\cdots,\bold{x_m}\}$,它总共有$m$个,每一个数据$\bold{x}$都是一个行向量,维度是$n$,那么第$i$个数据$\bold{x_i}$及其对应的标签$y_i$的形式如下:
(x_{i1},\cdots,x_{ij},\cdots,x_{in},y_i)
每一个数据$\bold{x}$都对应一个标签$y$,所有的标签集合在一起是一个维度为$(m,1)$的向量:
\bold{y}=(y_1,\cdots,y_i,\cdots, y_m)^T
(\bold{X},\bold{y})
=
(
\bold{x_{1}},\cdots,\bold{x_{i}},\cdots,\bold{x_{m}, \bold{y}}
)^T
=
\begin{bmatrix}
x_{11},\cdots,x_{1j},\cdots,x_{1n},y_1 \\
\cdots,\cdots,\cdots,\cdots,\cdots \\
x_{i1},\cdots,x_{ij},\cdots,x_{in},y_i \\
\cdots,\cdots,\cdots,\cdots, \cdots \\
x_{n1},\cdots,x_{nj},\cdots,x_{nj}, y_n
\end{bmatrix}
注意,上述矩阵一个行是一个数据,这样的表示与神经网络或深度学习中的表示不一致。
二、线性回归的表示
根据上述数据的高维形式,线性回归的目标是寻找一个超平面来最佳拟合上述数据,使得各个数据点的残差平方和最小。该超平面的形式如下:
\hat{y} = \bold{x} \bold{\beta}^T+b = \sum_{j=1}^n x_j\beta_j + \beta_0
也就是说,线性回归的目标是求出回归系数(regression coefficient),这也是一个行向量:
\bold{\beta} =(
\beta_1,
\cdots,
\beta_j,
\cdots,
\beta_n
)
和偏差$\beta_0$。而$\hat{y}$则是针对数据$\bold{x}$的预测结果。
\hat{\bold{y}} = \bold{X}\bold{\beta}^T+\bold{\beta}_0
这里的符号都加粗了,因此都是向量的形式。其中$\hat{\bold{y}}$表示预测结果,是维度$(m,1)$的向量,$\bold{X}$表示所有数据,其维度是$(m,n)$,$\bold{\beta}$是回归系数(regression coefficient),其维度是$(1,n)$,$\bold{w}^T$是$\bold{w}$的转置,因此,$\bold{\beta}^T\bold{X}$的结果的维度就是$(m,1)$,$\bold{\beta}_0$表示偏差,其维度也是$(m,1)$,其实这$m$个$\beta_0$都是一样的,因此:
\bold{\beta}_0 =
(
b,
\cdots,
b,
\cdots,
b
)
有的时候,我们会把预测的偏差也和回归系数放到一起:
\hat{y} = \bold{x}\bold{\beta}^T+\beta_0 x_0 = \sum_{j=0}^n \beta_j x_j
\bold{\hat{y}} = \bold{X}\bold{\beta}^T
亚马逊最新发布Feature Store简介

