BPR: Bayesian Personalized Ranking from Implicit Feedback论文简介及其笔记| 论文笔记好用的论文笔记工具

BPR: Bayesian Personalized Ranking from Implicit Feedback

小木 UAI 2009-09 6595 2017/02/14 22:15:49

# BPR（Bayesian Personalized Ranking）算法简介
基于项目的推荐是指为某个用户推荐一组个性化的项目列表。这篇文章研究了最常见的隐式反馈场景（implicit feedback）。基于隐式反馈的推荐应用有很多方法，如矩阵分解（matrix factorization, MF）或者最近邻（adaptive k-nearest-neighbor, kNN）。尽管这些方法都是求个性化排序的，但是他们并没有针对排序结果进行优化。这篇文章提出了一个一般性的优化标准，BPR-OPT，从贝叶斯分析的角度来获取最大化后验估计。作者也提出了一个关于BPR-OPT的一般性优化求解算法。该学习方法是基于随机梯度下降的bootstrap sampling。作者展示了本模型是如何应用在矩阵分解和kNN方法中的。

推荐系统是一个非常活跃的研究领域。当前大部分工作都是基于用户的显示反馈进行的，比如说评分。然而，现实生活中，有很多场景是只有隐式反馈的结果，比如点击流、观看次数、购买行为等。实际上，隐式反馈已经存在于几乎所有的信息系统中。这篇文章主要是利用隐式反馈解决推荐排序问题。

####问题描述
假设$U$是用户集合，$I$是项目集合。在本模型中，隐式反馈$S \subseteq U \times I$是可用的。比如购买行为，点击流等等。作者的目标是提供给用户一个个性化的推荐排序$>\_u \subset I^2$，其中$ >\_u$必须满足如下性质：
```math
\forall i,j \in I: i \neq j \Rightarrow i>_u j \vee j>_u i
```

```math
\forall i,j \in I: i >_u j \wedge j>_ui \Rightarrow i=j
```

```math
\forall i,j,k \in I: i >_u j \wedge j>_u k \Rightarrow i>_u k
```

分别称为总体性（totality），反对称性（antisymmetry），传递性（transitivity）。其实这个$>\_u$可以理解为什么东西在什么东西前面的意思，就是排序结果，可以理解为左边的项目比右边的项目靠前。为了简便，也有如下定义：
```math
I_u^+ := \{i\in I : (u,i) \in S \}
```
```math
U_i^+ := \{u\in U : (u,i) \in S \}
```
上面就是用户$u$给了饮食反馈的所有的项目，下面就是给印了项目$i$隐式反馈的所有用户。

####问题分析
如同之前的分析，饮食反馈系统只给了正向的可观测类别。剩下的数据是负向和缺失值的混合。对缺失值最常见的处理方法是忽略掉所有的内容，但是会导致机器学习算法无法学习到任何内容，而且算法也无法区别这两个级别的内容。最常见的推荐做法是针对某个项目计算一个个性化的得分$\hat{x}\_{ui}$，它反映了用户对该项目的偏好。然后推荐的项目结果可以使用该分值从大到小排序。典型的机器学习方法一般是从反馈集合$S$中创建一个训练集$(u,i) \in S$一个正向的标签，把剩下所有的作为负向的结果。也就是所有在集合$S$中的结果是1，剩下的结果是0。这里有个问题就是在训练过程中，所有在未来模型需要排序的没有反馈的结果以负向提供给了机器学习的算法。从而导致了尽管模型可以匹配训练集，但是对于预测结果为0的算法无法进行排序，这种算法能工作的唯一原因就是防止过拟合，即正则化（如图1所示）。
<center>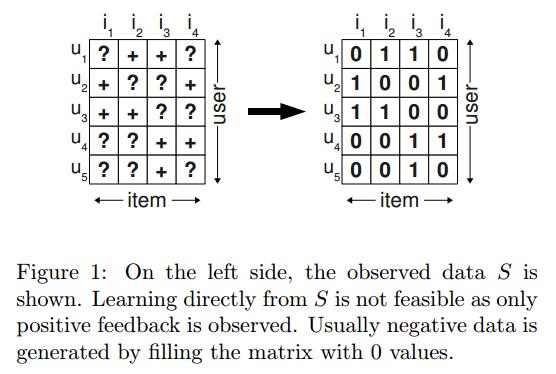
![](http://www.datalearner.com/resources/blog_images/6c6a0ac2-d2e8-4091-a2bb-ff45fb430bc0.jpg)
</center>

作者在这里提供了一个更好的方法，而不是简单的将用户未提供的信息作为负向案例处理。作者从集合$S$中为每个用户重新创建了一个排序$>\_u$。如果用户对一个项目$i$提供了一个隐式反馈，比如浏览，那么作者认为用户对这个项目的偏好要大于所有为观测的项目。比如在图2中，用户$u\_1$观看了项目$i_2$，但是没有观看项目$i_1$。那么作者假设，相比较项目$i_1$来说，这个用户更加倾向于选择项目$i_2$，即$i_2 >\_u i_1$。对于用户都看过的项目，我们则无法推断其偏好。形式化来说，作者创建了一个训练集$D_S: U \times I \times I$：
```math
D_S := \{ (u,i,j) | i \in I_u^+ \wedge j \notin  I_u^+ \}
```
这句话通俗理解就是用户$u$对$i$的偏好要大于对$j$的偏好。由于该排序是反对称性的，所以反过来就是负向的。
<center>![](http://www.datalearner.com/resources/blog_images/e1783459-9ea2-41f5-99db-a5db5d222eaa.jpg)</center>

作者的这个方法有两个好处：
1、作者的训练集由正向、负向和缺失值组成，两个未观测的项目之间的缺失值是最终需要预测的，并需要排序的结果。
2、该训练集的创建目标就是为了排序，即$>\_u$的观测子集$D_S$就是训练集。

####贝叶斯个性化排序
#####BPR优化准则
寻找所有项目的正确的个性化排序的贝叶斯形式就是要任意给定的模型参数$\Theta$的条件下求得如下后验的最大化：
```math
p(\Theta|>_u) \propto p(>_u|\Theta)p(\Theta)

```
这里的$>\_u$是我们想要求得的排序目标，但是是无法观测的结果，我们假设所有用户之间相互独立。同样的，我们也假设对于每一个用户$u$的某一个项目对$(i,j)$之间也是相互独立的。因此上式的似然函数可以写成：
```math

\prod _{u\in U} p(>_u|\Theta) = \prod_{(u,i,j)\in U \times I \times I} p(i>_uj|\Theta)^{\sigma((u,i,j) \in D_S)} \cdot (1-p(i>_u|\Theta))^{\sigma((u,i,j) \notin D_S)}

```
其中，$\sigma$是指示函数：
```math

\sigma(b) =

\begin{cases}

1 \space \textbf{if b is true} \\
0 \space \textbf{else}

\end{cases}
```

由于总体性和反对称性，上式也可以简化成：
```math

\prod_{u \in U} p(>_u | \Theta) = \prod_{ (u,i,j)\in D_S } p(i>_u j|\Theta)

```

到目前为止，我们还没有建立排序的结果。这里假设用户对项目$i$和$j$之间的真正的偏好为：
```math
p( i>_u | \Theta) := \sigma(\hat{x}_{uij}(\Theta))
```
其中$\sigma$是logistic sigmoid函数：
```math
\sigma(x) := \frac{1}{1+e^{-x}}
```
在这里，$\hat{x}\_{uij} (\Theta)$是模型参数向量$\Theta$的任意一个实值函数，主要是描述用户$u$与项目$i$与项目$j$之间的关系。换句话说，本模型就是为了给这三者之间的关系进行建模，最终是估计$\hat{x}\_{uij} (\Theta)$。因此，为个性化的排序$>\_u$进行统计建模是可行的。到目前为止，我们讨论的都是似然函数。进一步的，我们假设先验密度$p(\Theta)$是一个均值为0协方差矩阵为$\sum\_{\Theta}$的正态分布：
```math
p(\Theta) \sim N(0,\sum_{\Theta})
```
同时，为了减少未知参数的数量，我们设置$\sum\_{\Theta}=\lambda\_{\Theta}I$。于是我们最终的BPR-OPT的结果就是：
```math
\begin{aligned}
\textbf{BPR-OPT} & :=  \ln p(\Theta|>_u) \\
 & = \ln p(>_u|\Theta)p(\Theta) \\
 & = \ln \prod_{(u,i,j) \in D_S} \sigma( \hat{x}_{uij} )p(\Theta) \\
 & = \sum_{(u,i,j)\in D_S} \ln \sigma( \hat{x}_{uij} ) + \ln p(\Theta) \\
 & = \sum_{(u,i,j)\in D_S} \ln \sigma( \hat{x}_{uij} ) - \lambda_{\Theta}||\Theta||^2
\end{aligned}
```
其中$\lambda\_{\Theta}$是正则化参数。

赏

支付宝扫码打赏

如果文章对您有帮助，欢迎打赏鼓励作者