多元高斯分布（多元正态分布）简介

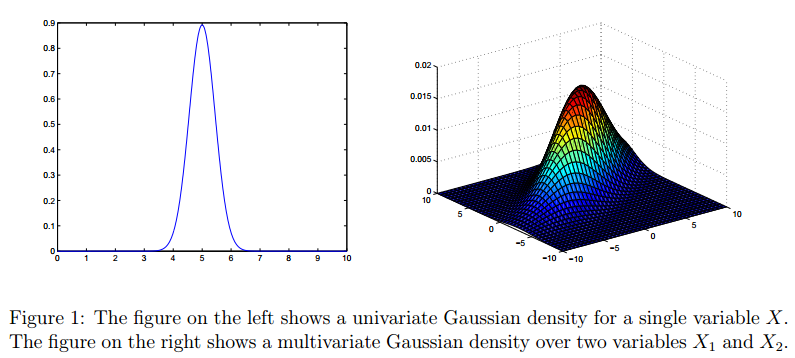
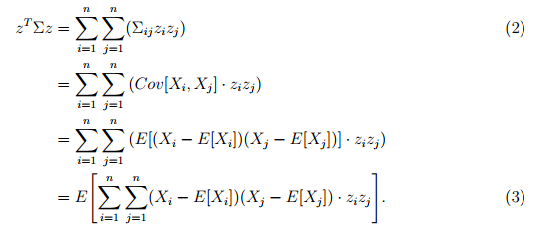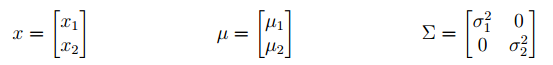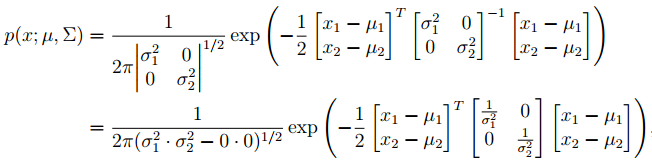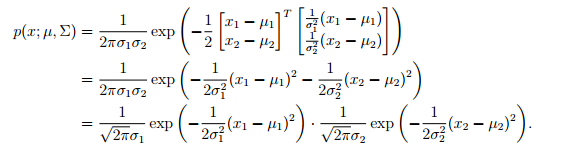高斯分布（Gaussian Distribution），也称作是正态分布（Normal Distribution），是一种非常常见的分布，对于一元高斯分布（Univariate Gaussian Distribution）我们比较熟悉，对于高斯分布的多元形式有很多人不太理解。我们将简单介绍一下多元高斯分布的相关性质。这篇博客的材料主要来源Andrew Ng在斯坦福机器学习课的材料。[[1]][1] [1]: http://cs229.stanford.edu/materials.html "斯坦福机器学习课程材料"

多元高斯分布（Multivariate Gaussian Distribution）的形式很简单，就是一元高斯分布的在向量形式的推广。我们把向量$X=[X_1,X_2,...,X_n]^T$称作是均值为$\mu \in \bold{R}^n$，协方差矩阵为$\Sigma \in S^n$的多元高斯分布，如果它具有如下概率密度函数的形式：

p(x;\mu , \Sigma)=\frac{1}{(2\pi)^{n/2}|\Sigma|^{1/2}}\exp(-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu))

#### 一、多元高斯分布与一元高斯分布的关系 首先，我们回顾一下一元正态分布的形式，其概率密度函数如下： ```math p(x;\mu,\sigma^2)=\frac{1}{\sqrt{2\pi}\sigma}\exp(-\frac{1}{2\sigma^2}(x-\mu)^2) ``` 这里指数函数的参数$(-\frac{1}{2\sigma^2}(x-\mu)^2)$是一个关于x的二次项式函数。由于二次项的系数为负，因此它是抛物线开口向下的函数。此外，最前面的系数是$\frac{1}{\sqrt{2\pi}\sigma}$是与x无关的形式，因此我们可以把它当做是一个“正规化因子”（normalization factor），以保证： ```math \frac{1}{\sqrt{2\pi}\sigma}\int_{-\infty}^{\infty}\exp(-\frac{1}{2\sigma^2}(x-\mu)^2)=1 ``` 在多元高斯密度中，指数函数的参数是$-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu)$，其中x是向量。由于$\Sigma$是正定的（positive definite），而任意正定矩阵的逆矩阵也是正定的。那么对于任意一个非零向量z，有$z^T \Sigma z>0$，也就是说对于任意的$x \neq \mu$，有： ```math (x-\mu)^T\Sigma^{-1}(x-\mu) > 0 ``` ```math -\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu) < 0 ``` 与一元高斯分布类似，我们可以把该指数函数的参数当做一个开口向下的二次曲面（downward opening quadratic bowl）。在多元高斯密度函数中，前面的系数的形式比一元高斯分布要复杂很多，但它也同样的不依赖于x。因此，它也是一个正规化系数：