强化学习基础之马尔可夫决策过程（Markov Decision Processes）和马尔可夫奖励过程（Markov Reward Processes）

强化学习（Reinforcement Learning）发展密切相关的一个方法就是马尔可夫决策过程（Markov Decision Processes，MDPs），这是一种离散随机过程（discrete-time stochastic control processes），它提供了一个数学框架，用于在结果部分是随机的、还有部分受决策者控制的情况下对决策进行建模。说白了，就是一种问题建模方法。它不是一种解决方法，而是针对某些问题进行建模，一旦建模完成，就可以使用例如动态规划的方法来解决这些问题。

马尔可夫决策过程可以用来描述强化学习的“环境”，且这个环境是完全可观测的（fully observable）。几乎所有的强化学习问题都可以用MDPs来形式化：

• 最优控制可以使用连续MDPs来处理
• 部分可观察问题可以转换成MDPs
• 赌博机（Bandits）问题是有一个状态的MDPs

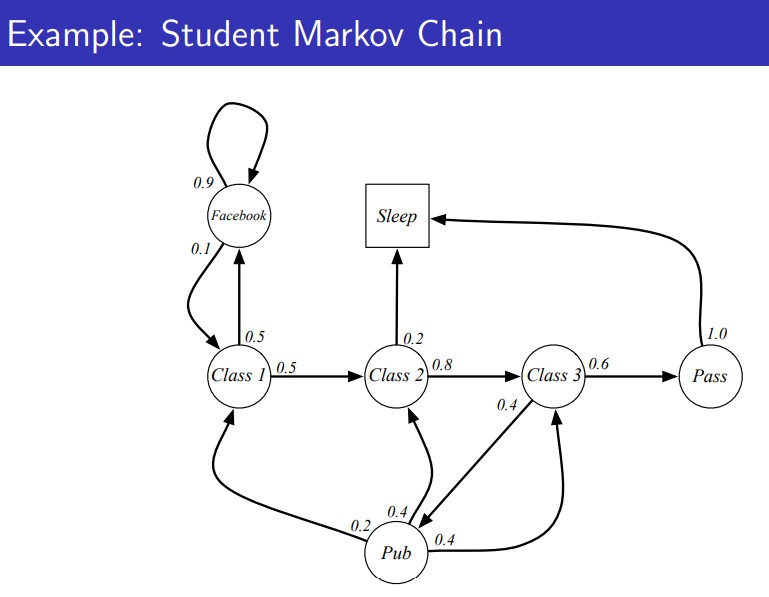
因此，马尔可夫决策过程对于学习强化学习来说是必不可少的基础部分。本文将简要介绍这个模型及其变种马尔可夫奖励过程（Markov Reward Processes）。为了帮助理解马尔科夫决策过程，我们将从问题例子入手，讲述如何使用这个方法对问题进行建模。