逻辑回归详解（Logistic Regression）【含Java/Python代码】

逻辑回归（Logistic Regression）是一种应用非常广泛的回归方法，它使用逻辑函数为二元依赖变量的数据建模，即标签或者依赖变量只有0和1两种情况，因此可以作为二分类的模型使用。同时，逻辑回归也可以看做是没有隐藏层且激活函数为Sigmoid函数的神经网络。它是很多模型的基础。

我们以iris数据集为例，总共有5列，前四列是花的属性，分别是 Sepal.Length（花萼长度）； Sepal.Width（花萼宽度）; Petal.Length（花瓣长度）; Petal.Width（花瓣宽度）;

最后一列是花的种类，分别是 Iris Setosa（山鸢尾） - 0； Iris Versicolour（杂色鸢尾） - 1； Iris Virginica（维吉尼亚鸢尾） - 2；

样例如下（我们已经最后一列转换成了0和1形式，为了便于分析逻辑回归，我们去掉了2这一种）：

5.1,3.5,1.4,0.2,0.0
4.9,3.0,1.4,0.2,0.0
4.7,3.2,1.3,0.2,0.0
4.6,3.1,1.5,0.2,0.0
5.0,3.3,1.4,0.2,0.0
7.0,3.2,4.7,1.4,1.0
6.4,3.2,4.5,1.5,1.0
6.9,3.1,4.9,1.5,1.0
5.5,2.3,4.0,1.3,1.0
6.5,2.8,4.6,1.5,1.0

为了根据花的形状来预测花的种类，我们可以使用逻辑回归来判断。

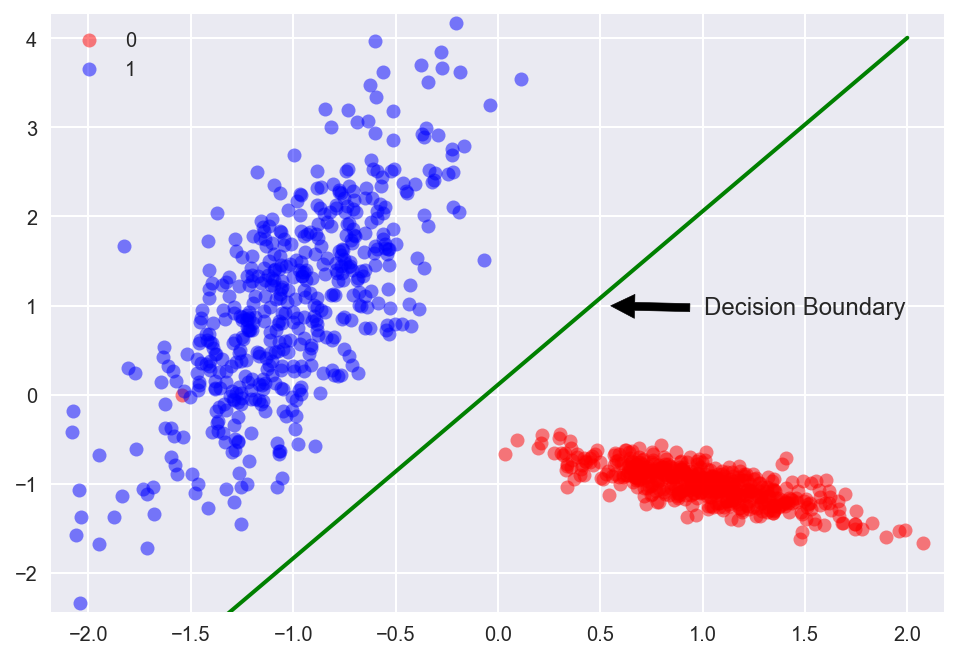
以二维数据为例，逻辑回归的目的就是找出一条直线，将二维平面上的点分成两部分：