梯度下降是一种迭代优化的方法，它的目标是求解一个函数的最小值。我们以一个简单的例子来说明。

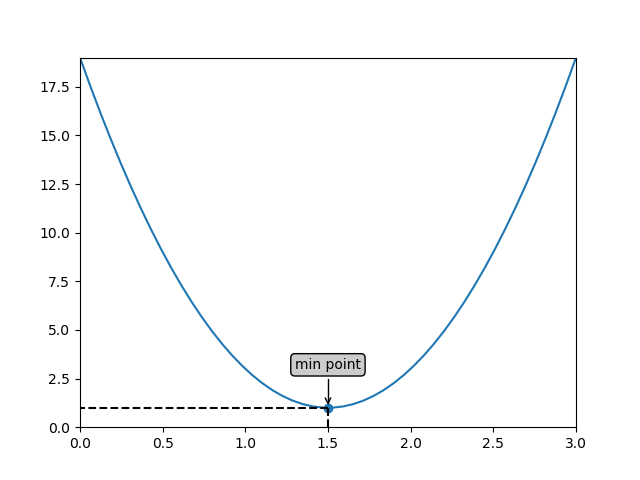
例如，如上图所示，这是一个二次函数的图像：

y = 8(x-1.5)^2 + 1

其最低点是(1.5,1)。我们希望找到这个最低点。其实，对于这个简单的二次函数，我们只要求y对x的导数，并令其结果为0即可求出最低点。为了说明梯度下降的原理，我们不采用这种方式。

一、梯度下降（Gradient Descent）的原理

梯度下降的原理就是初始随机选择一个函数上的点，然后沿着某个方向运行选择下一个函数上的点，使得下一个点的函数值比上一个点的函数值小，这样不停迭代直到找到最小值位置。那么，这里有可能有三个问题需要注意

• 首先，为什么不使用刚才说的求导方式找最小值？这是因为并不是所有的函数都容易求导，例如对于多元函数来说，就很难，但是梯度下降的原理则依然有效。
• 其次，什么样的函数可以使用梯度下降求解？需要这个函数是凸函数，这样我们才能找到全局最小值，否则就无法确保找到最小值，因为其结果可能是极值。
• 最后，沿着什么方向寻找下一个点才是正确的，且速度最快？这就是梯度下降的核心概念：沿着梯度的方向才是最正确的方向。

如下图所示，我们随机选了一个函数图像上的点（initial point），假设为(2.5,9)。这个时候，寻找下一个点的方向就有两个了，一个是向上（up），另一个是向下（down）。显然，我们应该往下方走才是正确的方向。

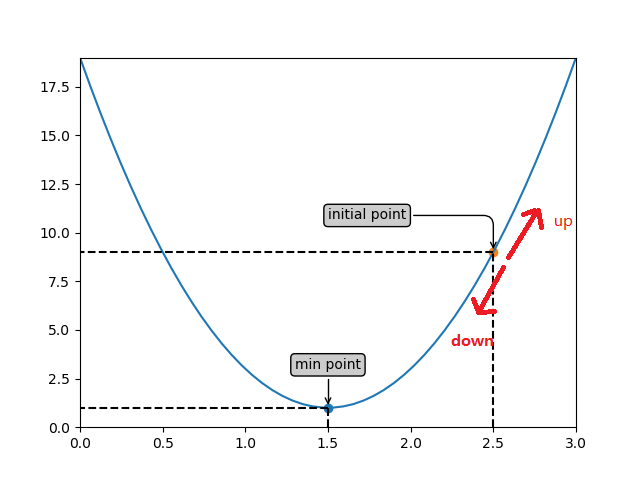
梯度下降的原理其实就是告诉我们让凸函数上的任意一点沿着梯度的方向向下就可以找到最低点了（注意，有的人说我要找的是最大值，那你就把函数加个负号，这样图形就转换过来变成找最小值了，这种简单问题不说了）。

二、什么是梯度（Gradient）？

“A gradient measures how much the output of a function changes if you change the inputs a little bit.” — Lex Fridman (MIT)

也就是说它只是根据误差的变化来衡量所有权重的变化。 简单点说就是斜率，函数图像最陡峭的地方，也就是函数对某个权重（x）求偏导之后的方向。还是以上图为例，在最低点的左侧，函数的斜率是负值，那么左侧的横坐标的点减去梯度，它将往右侧移动，那么y的值是下降的。在右侧正好反过来了，其梯度是正值，那么最低点右侧的点减去梯度会使得这个点往左移动，这样也使得y值下降。因此，梯度就是斜率，那点的坐标轴的值减去这个梯度就能使得函数值下降，进而帮助我们寻找最小值。

刚才说的是坐标点减去梯度的方向一定是往最小值移动的，不仅如此，梯度还有个最陡峭的概念，函数上的点往任何一个方向移动都不如向梯度方向移动的时候其值下降得快。以下图为例：

中间红色的就是梯度的方向，那么下山最快，其他发现虽然也可以下山，但是多走了很多弯路。在我们的上面的函数中，就是下图红色虚线的方向是梯度了：

三、数学化描述

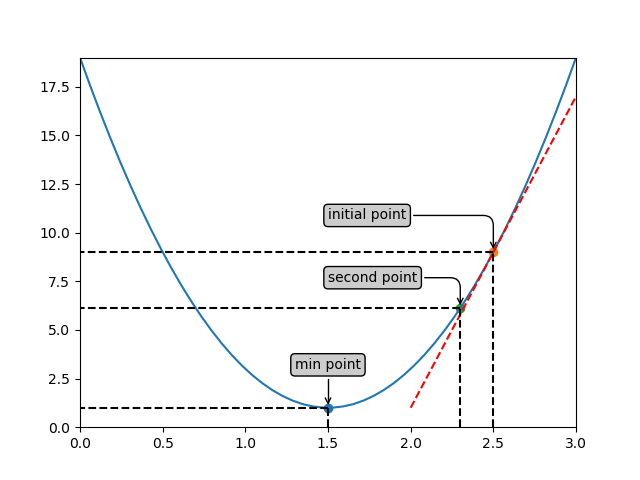
下面我们来用数学语言描述一下梯度下降。假设我们有一个凸函数：

y = f(x)

其形式比较复杂无法直接求出最小值，我们来使用梯度下降的方法求其最小值。那么，首先我们要计算梯度：

\nabla f(x) = \frac{dy}{dx}

使用梯度下降的时候，第一步要随机选择一个初始点，如(x_0,y_0)，然后，利用沿着梯度的方向搜索寻找下一个点：

x_1 = x_0 - \alpha \nabla f(x_0)

y_1 = f(x_1)

这样我们就得到了下一个点，这时候我们计算一下y_1-y_0，如果结果很小，那么说明我们已经接近底部，即最小值了，通常我们只要这个近似最小值就可以了。

在机器学习中，我们有很多求最小值的问题，因为我们有很多机器学习的任务都有一个目标函数，需要求目标函数的最小值已达到最好的拟合效果。以回归分析为例，一般的线性回归分析的方程如下：

\hat{y} = \sum_{j=0}^n w_jx_j

一般情况下，我们有m个训练集，我们的目标函数是一个残差平方和：

\begin{aligned} J(\bold{w}) &= \frac{1}{2m} \sum_{i=1}^m (\hat{y_i} - y_i)^2 \\ & \\ &= \frac{1}{2m} \sum_{i=1}^m (\sum_{j=0}^n w_jx_{ij} - y_i)^2 \\ \end{aligned}

我们希望求出这个目标函数的最小值，这是无法直接求导得出结论的，因此我们可以使用梯度下降来求解，这个函数的梯度为：

\nabla = \frac{\partial J}{\partial w_j} = \frac{1}{m} \sum_{i=1}^m (\sum_{j=0}^n w_jx_{ij} - y_i) x_{ij}

四、三种不同的梯度下降方法

如前所述，这个梯度是对第j个参数的梯度，我们有m个训练集。实际上，梯度下降一半有三种：批量梯度下降（Batch Gradient Descent）、随机梯度下降（Stocahstic Gradient Descent, SGD）和小批量梯度下降（Mini-Batch Gradient Descent, MBGD）。我们分别介绍。

4.1、批量梯度下降（BGD）

批量梯度下降（也称为原始梯度下降）计算训练数据集中每个样本的误差，但是每次更新参数都会使用所有的训练样本：

w_j' = w_j - \frac{1}{m} \sum_{i=1}^m (\sum_{j=0}^n w_jx_{ij} - y_i) x_{ij}

它的优点是它具有计算效率，它可以产生稳定的误差梯度和稳定的收敛。 批量梯度下降的缺点是稳定的误差梯度有时会导致收敛状态不是模型可以达到的最佳状态。 它还要求整个训练数据集在内存中并可供算法使用。也就是说对内存的要求很高。每一次迭代下对每个参数进行更新的时候，都要计算所有的数据，因此在样本数量很大的时候比较耗时。

4.2、随机梯度下降（SGD）

相反，随机梯度下降（SGD）对数据集中的每个训练样本都进行更新操作。这意味着它会逐个更新每个训练样本的参数。这可以使SGD比批量梯度下降更快，具体取决于问题。 一个优点是频繁的更新使我们有一个非常详细的改进率。

事实上，频繁更新作为批量梯度下降的方法在计算上更加昂贵。这些更新的频率也可能导致噪声梯度，这可能导致错误率跳跃，而不是缓慢下降。因此，它的下降过程是个杂乱的过程，看起来没有顺序。

以上述为例，我们写出每个样本（这里以第i个样本为例）的目标函数（损失函数）：

\frac{1}{2} (\sum_{j=0}^n w_jx_{ij} - y_i)^2

每个样本都会更新所有的参数：

w_j' = w_j - (\sum_{j=0}^n w_jx_{ij} - y_i) x_{ij}

随机梯度下降在每一次迭代的时候，先循环每个样本，对每个样本都更新所有的权重。

4.3、小批量梯度下降（MBGD）

小批量梯度下降是首选方法，因为它结合了随机梯度下降（SGD）和批量梯度（BGD）下降的概念。 它只是将训练数据集拆分成小批量，并为每个批次执行更新。 因此，它在随机梯度下降的稳健性和批量梯度下降的效率之间创造了平衡。

常见的小批量大小介于50到256之间，但与任何其他机器学习技术一样，没有明确的规则，因为它们可能因不同的应用而异。 请注意，它是您训练神经网络时的首选算法，它是深度学习中最常见的梯度下降类型。

它的迭代首先需要将样本数据划分成很多个组，对每一次迭代来说，先循环所有的组，对每个组内的数据采用批量梯度下降的方式循环。

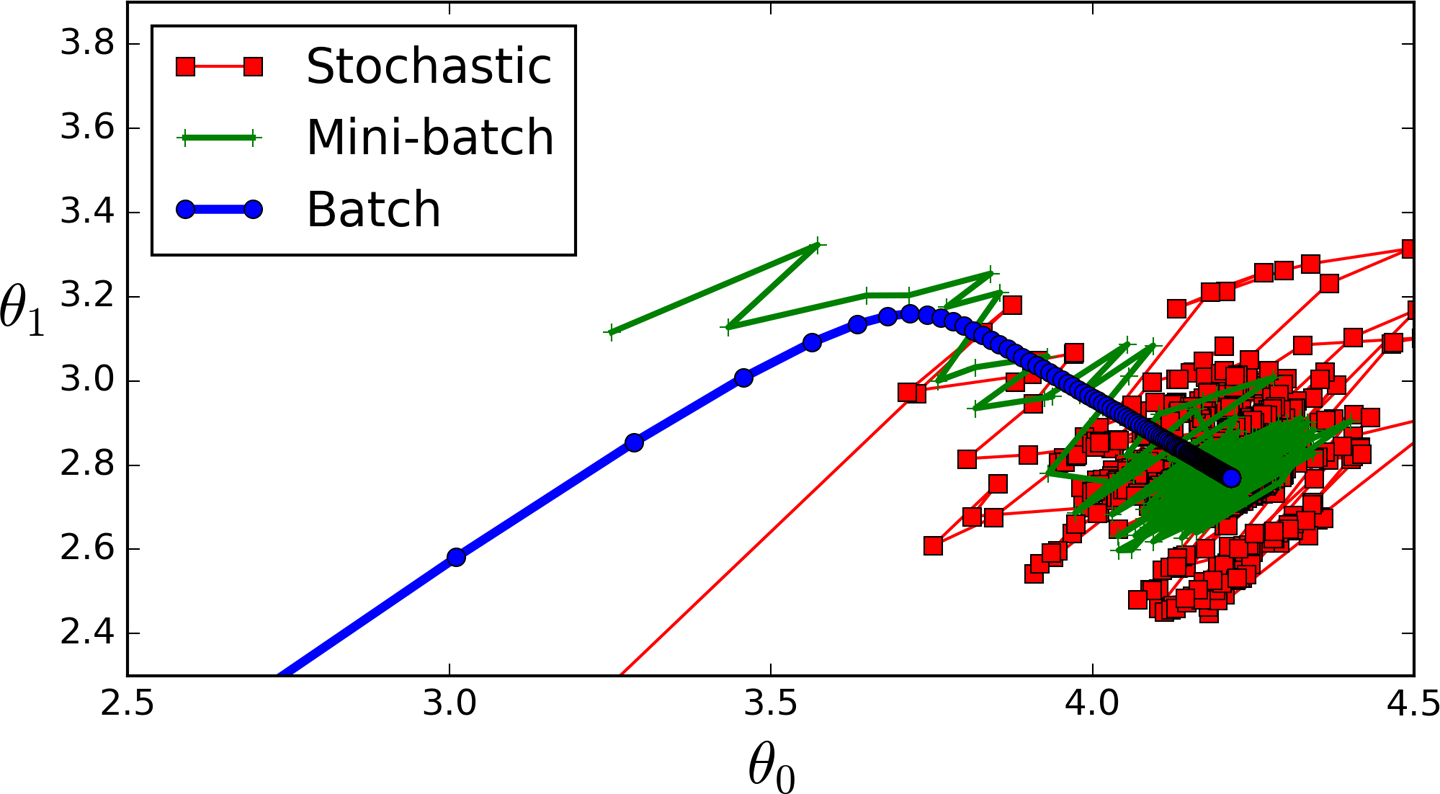
总结一下，随机梯度下降可能不是很快能找到最优的结果，因为它是跳跃着进行的，而批量梯度下降能快速的找到最优解，但是对内存要求较高。如下图所示是三种不同梯度下降的运行情况：