
标签为 #R# 的博客
聚焦人工智能、大模型与深度学习的精选内容,涵盖技术解析、行业洞察和实践经验,帮助你快速掌握值得关注的AI资讯。
最新博客





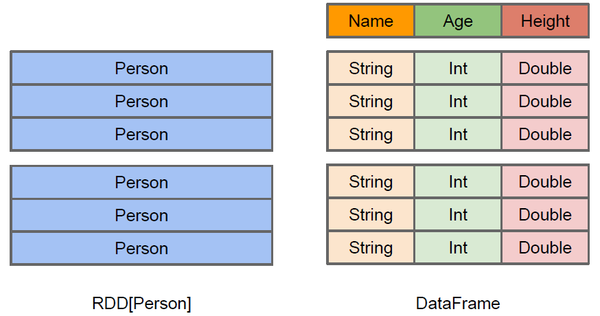
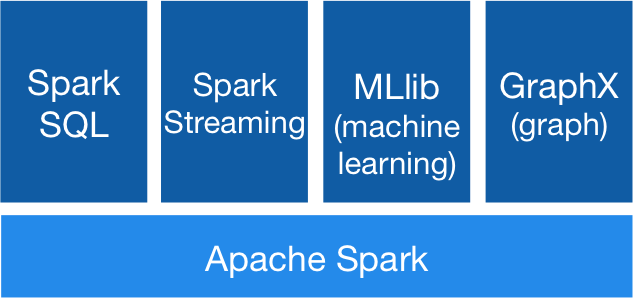
Spark源码分析之RDD下的KMeans
这篇博客主要介绍Spark源码中的KMeans部分,说的是RDD下的KMeans源码

stata 用outreg2输出回归结果
stata 输出回归结果


keras解决多标签分类问题
multi-class classification problem和 multi-label classification problem在keras上的实现

如何理解狄利克雷过程(Dirichlet Process)
狄利克雷过程是非参贝叶斯推断的基础模型。本博客将简要介绍狄利克雷过程模型

origin绘图操作案例(1)
日常绘图时,会使用都origin,其是一款非常强大的制图工具
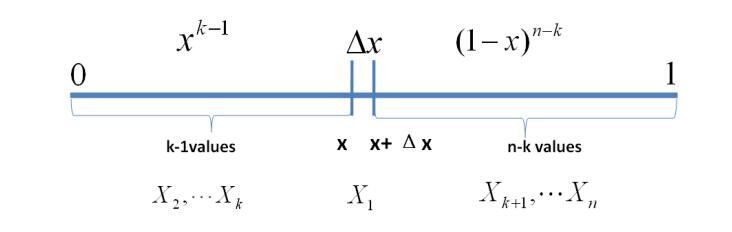
Dirichlet Distribution(狄利克雷分布)与Dirichlet Process(狄利克雷过程)
Dirichlet过程是一个随机过程,在非参数贝叶斯模型中有广泛运用,最常见的应用是Dirichlet过程混合模型
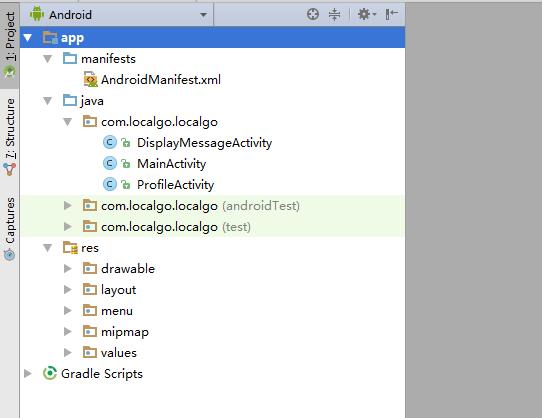
Android开发入门基础
Android是基于Linux的修改版本的移动操作系统。 大多数Android代码是在开源Apache许可证下发布的。本文将简单介绍Android开发入门知识。

Android开发入门基础知识——Intent详解
Intent是Android中通信的组件。这篇博客将详细讲述什么是Intent及其用法。
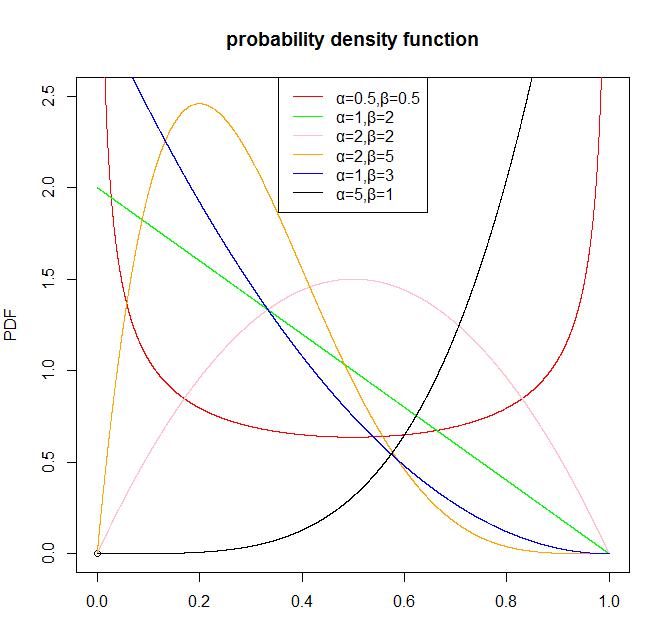
贝塔分布(Beta Distribution)简介及其应用
贝塔分布(Beta Distribution)是一个连续的概率分布,它只有两个参数。它最重要的应用是为某项实验的成功概率建模。在本篇博客中,我们使用Beta分布作为描述。
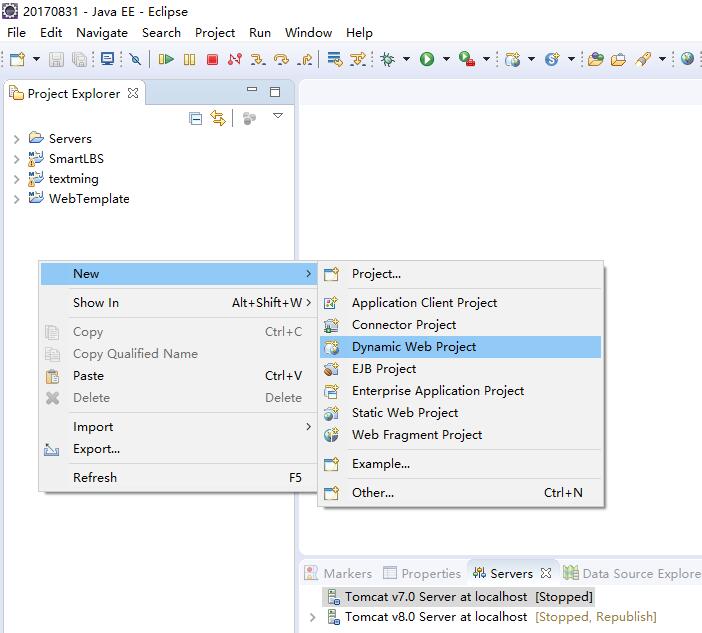
使用SpringMVC创建Web工程并使用SpringSecurity进行权限控制的详细配置方法
使用SpringMVC框架搭建Web项目工程是目前非常流行的web项目创建方式。同时Spring Security也为我们提供了登录验证和权限控制等内容。
使用Spring Security进行登录验证
Spring Security可以帮助我们进行页面的权限控制和登录验证,在这篇博客中,我们将简要描述如何使用Spring Security进行登录验证。

Android开发中常见错误及其解决方法
在Android开发中,我们经常会遇到很多问题,这里记录了一些常见的问题及其解决方法

Wishart分布简介
Wishart分布在多元高斯的贝叶斯推断中非常重要。它通常作为正态分布的协方差矩阵的逆矩阵的共轭先验存在。这篇博客将详细讲述Wishart分布及其作用。

Python之numpy.argpartition
神秘的numpy.argpartition

编程项目构建工具简介
在进行编程操作的时候,我们常常会遇到很多与编程无关的项目管理工作,如下载依赖、编译源码、单元测试、项目部署等操作。一般的,小型项目我们可以手动实现这些操作,然而大型项目这些工作则相对复杂。构建工具是帮助我们实现一系列项目管理、测试和部署操作的工具。本文将对Java构建工具做简单介绍。
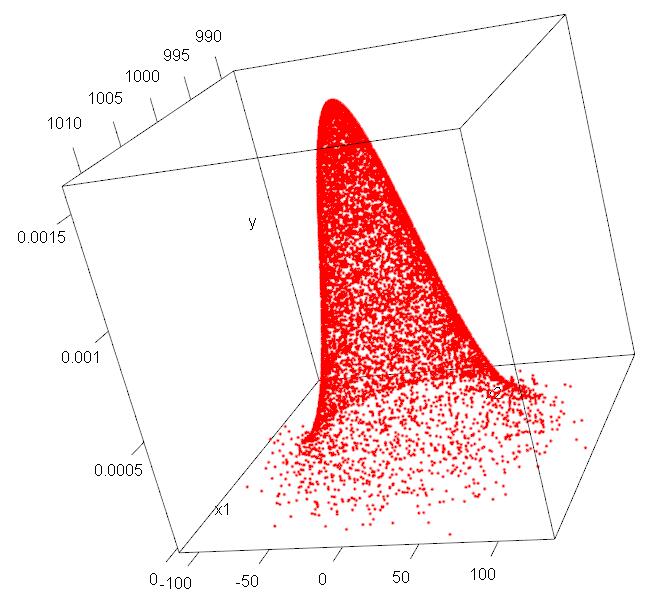
R语言技巧总结笔记
蛋疼的R语言
![[翻译]应用到文本领域的卷积方法](https://www.datalearner.com/resources/blog_images/datalearner_blog_default_img.jpg)
[翻译]应用到文本领域的卷积方法
本文介绍了文本领域的相关任务和技术,探讨了循环神经网络在文本领域的优势,并进一步研究了应用在文本领域的卷积网络方法,原文地址:https://medium.com/@TalPerry/convolutional-methods-for-text-d5260fd5675f