CNN中的一些高级技术（空洞卷积/显著图/反卷积）
11,159 阅读
加载中...
加载中...
卷积神经网络是图像识别领域最重要的深度学习技术。也可以说是是本轮深度学习浪潮开始点。本文总结了CNN的三种高级技巧，分别是空洞卷积、显著图和反卷积技术。原文发布在[Medium](Advanced Topics in Deep Convolutional Neural Networks)。
CNN的独特方面如下：
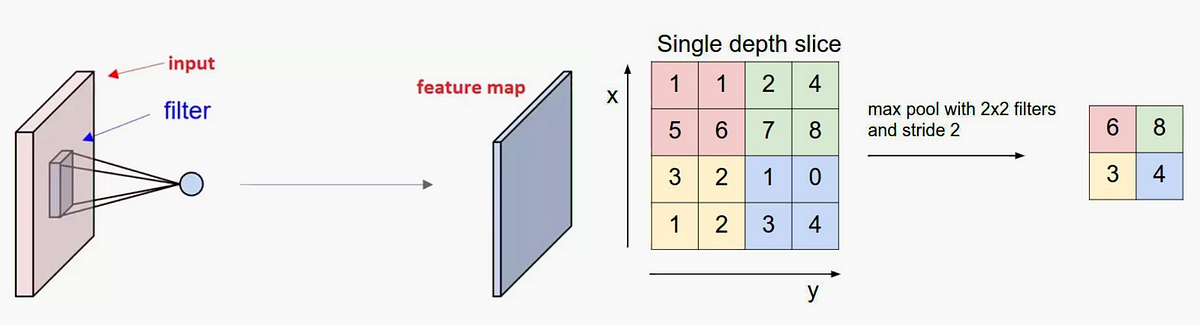
卷积层由滤波器（filters），特征映射（feature maps）和激活函数（activation function）组成。
如果输入的维度已知，我们可以确定卷积块的输出的维度。这个计算方法可以参考《深度学习卷积操作的维度计算》。
池化层用于减少过拟合。全连接的层用于将空间和通道特征混合在一起。每个滤波层都和feature map抽取的图像对应，这就是提取特征的方式。
知道输入和输出层的数量很重要，因为这决定了构成神经网络参数的权重和偏差的数量。 网络中的参数越多，需要训练的参数越多，导致训练时间越长。训练时间对于深度学习非常重要，因为它是一个限制因素，除非您可以访问强大的计算资源，如计算集群。
下面是一个示例网络，我们将为其计算参数总数。
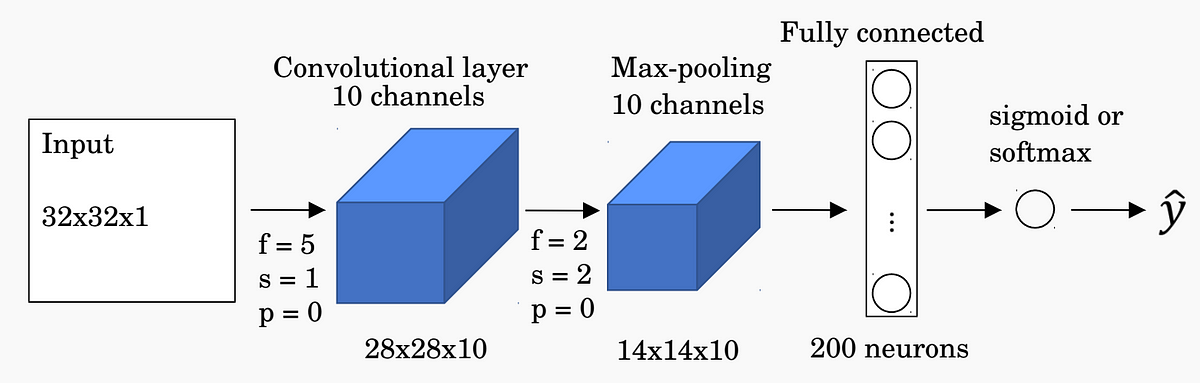
在这个网络中，我们在卷积滤波器上有250个权重和10个偏差项。 我们在max-pooling层上没有权重。 在最大池化层之后，我们有13×13×10 = 1,690个输出元素。 我们有一个200节点的完全连接层，在完全连接层中总共产生1,690×200 = 338,000个权重和200个偏置项。 因此，我们在网络中共有338,460个参数需要接受训练。 我们可以看到大多数训练的参数出现在完全连接的输出层。
每个CNN层都学习越来越复杂的滤波器。 第一层学习基本特征检测滤波器，例如边缘和角落。 中间层学习检测对象部分的滤波器 - 对于面部，他们可能学会对眼睛和鼻子做出反应。 最后的图层具有更高的表示形式：它们学习识别不同形状和位置的完整对象。
感受野被定义为输入空间中特定CNN的特征正在观察（即受其影响）的区域。 在5×5输入映射上应用内核大小为k = 3×3，填充大小为p = 1×1，步长s = 2×2的卷积C，我们将得到一个3×3输出特征映射（绿色映射）。
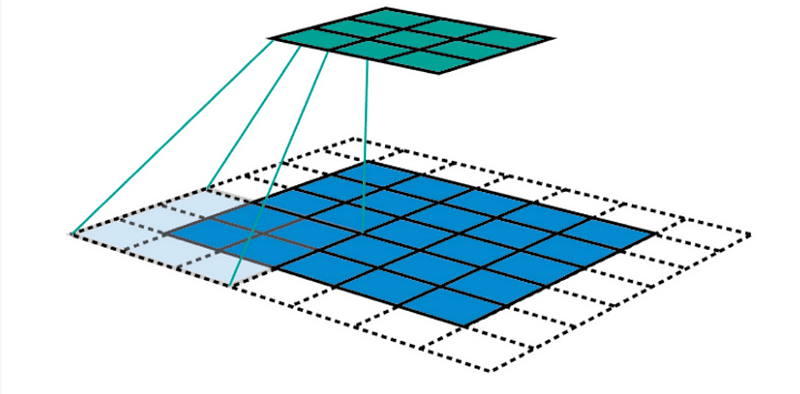
在3×3特征图之上应用相同的卷积，我们将得到2×2特征图（橙色图）。
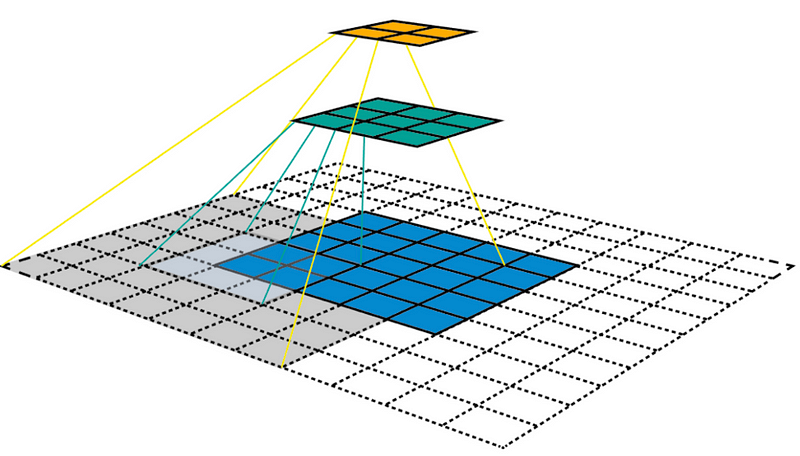
让我们再次以一维方式看待感受野，没有填充，步长为1，内核大小为3×1。
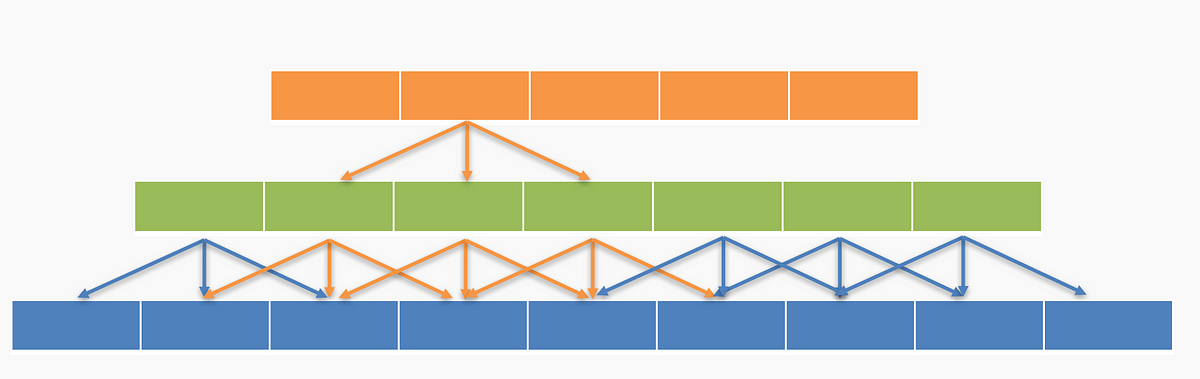
我们可以跳过其中一些连接以创建空洞卷积（Dilated Convolutions），如下所示。
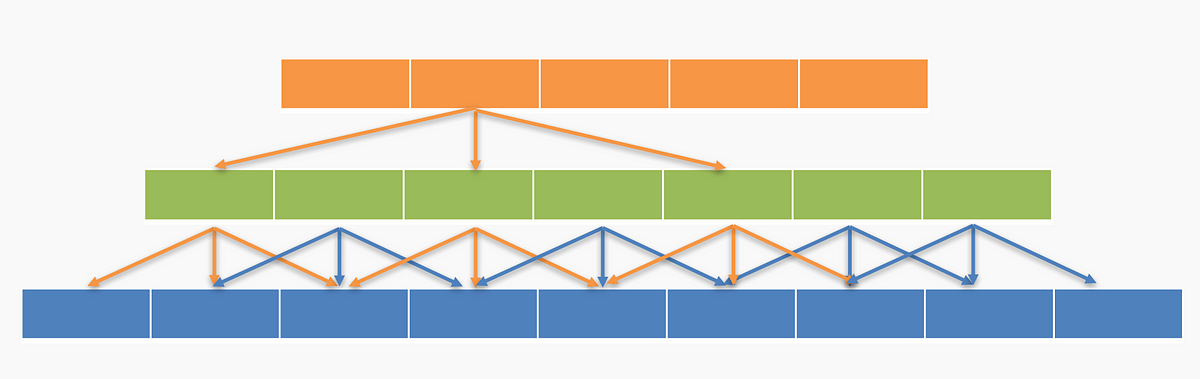
空洞卷积以与正常卷积类似的方式工作，主要区别在于感受野不再由连续像素组成，而是由其他像素分开的各个像素组成。 扩散卷积层应用于图像的方式如下图所示。
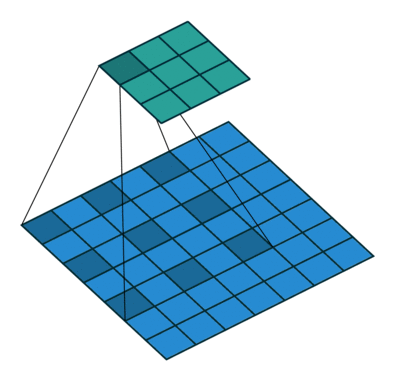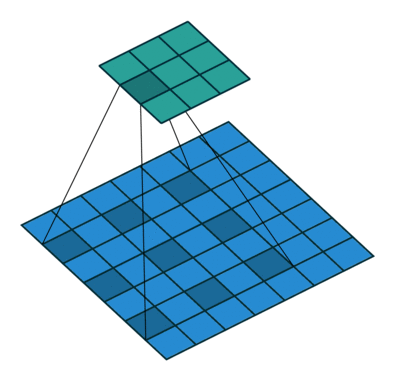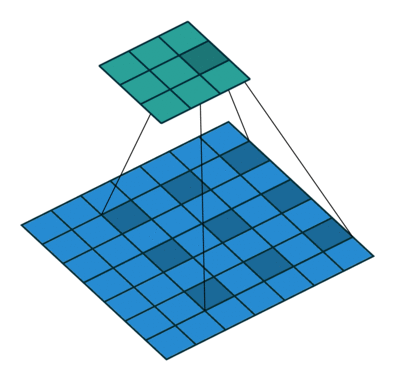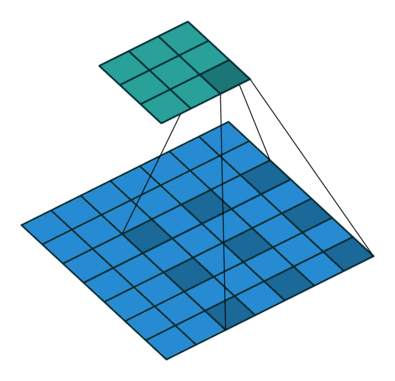
下图显示了二维数据的空洞卷积。 红点是过滤器的输入，其为3×3，绿色区域是由这些输入中的每一个捕获的感受野。 感受野是每个输入（单位）到下一层的初始输入上捕获的隐含区域。
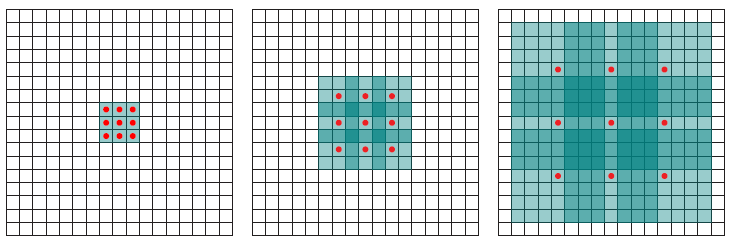
使用空洞卷积背后的动机是：
在下一节中，我们将讨论使用显着性映射来检查卷积网络的性能。
显著图是数据科学家用于检查卷积网络的有用技术。 它们可用于研究神经元的激活模式，以查看图像的哪些特定部分对于特定特征是重要的。
让我们想象一下，你会得到一张狗的图像并要求对它进行分类。 这对于人类来说非常简单，但是，深度学习网络可能不像你那么聪明，而是可能将其归类为猫或狮子。 为什么这样做？
网络可能错误分类图像的两个主要原因：
我们想要了解是什么让网络将某个类作为输出 - 这样做的一种方法是使用显著图。 显著图是一种测量给定图像中特定类的空间支持的方法。
“当我通过我的网络传输图像时，找到负责C类分数S（C）的像素”。
我们怎么做？ 我们使用区别（differentiate）！ 对于任何函数f（x，y，z），我们可以通过在该点找到关于这些变量的偏导数，找到变量x，y，z对任何特定点（x 1，y 1，z 1）的影响。 类似地，为了找到负责的像素，我们对C类取分数函数S，并对每个像素取偏导数。
这很难自己实现，但幸运的是，auto-grad可以做到这一点！ 该程序的工作原理如下：
注意：在步骤＃2中，我们将其转换为二进制分类并使用概率，而不是执行softmax。
以下是显着性图的一些示例。
我们如何处理彩色图像？ 获取每个通道的显着图，并采用最大值，平均值或使用所有3个通道的方式显示。
概述显着图的功能的两篇好文章是：
Deep Inside Convolutional Networks: Visualising Image Classification Models and Saliency Maps
Attention-based Extraction of Structured Information from Street View Imagery
有一个与本文相关的GitHub库，其中我将展示如何生成显着图（可以在此处找到库）。
到目前为止，我们所看到的卷积要么保持其输入的大小，要么使其变小。 我们可以使用相同的技术使输入张量更大。 此过程称为upsampling。 当我们在卷积步骤中进行时，它被称为反卷积（transposed convolution）或微步卷积（fractional striding）。
注意：有些作者在使用反卷积时会称之为upsampling，但该名称已经采用了以下文章中概述的不同概念：
https://arxiv.org/pdf/1311.2901.pdf
为了说明反卷积的工作原理，我们将看一些卷积的例子。
第一个是没有填充的典型卷积层的示例，作用于大小为5×5的图像。在卷积之后，我们最终得到3×3图像。
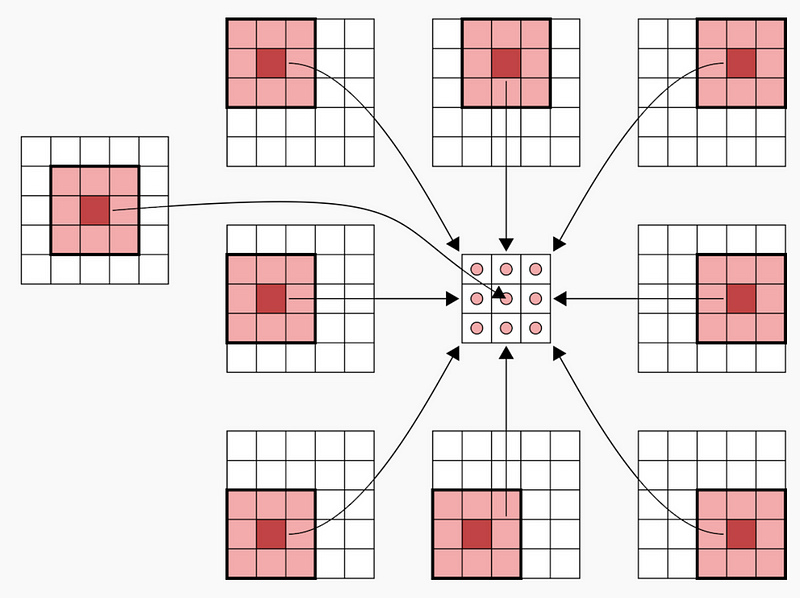
现在我们看一个填充为1的卷积层。原始图像是5×5，卷积后的输出图像也是5×5。
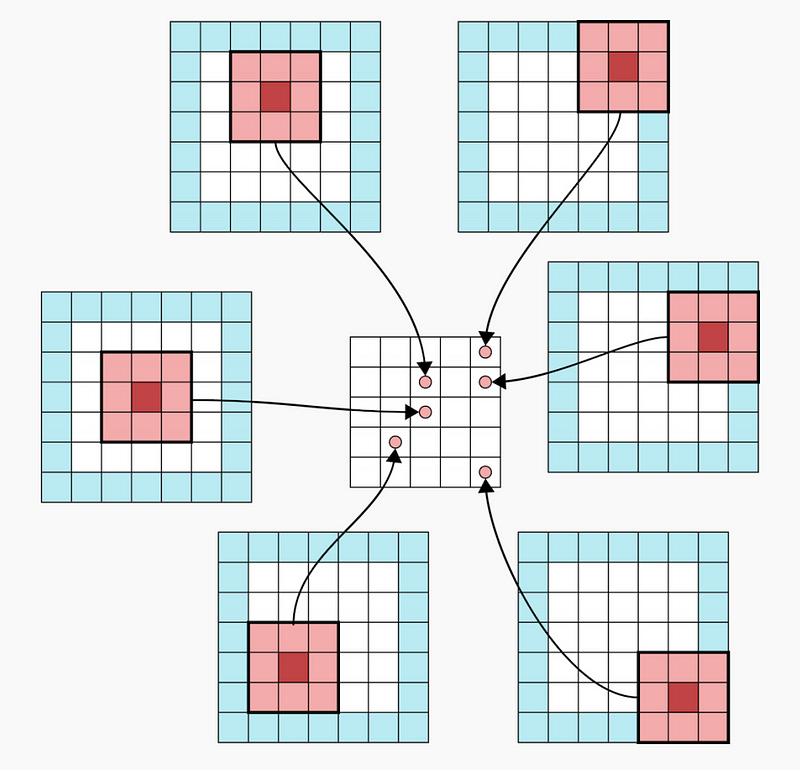
现在我们看一个填充为2的卷积层。原始图像是3×3，卷积后的输出图像也是5×5。
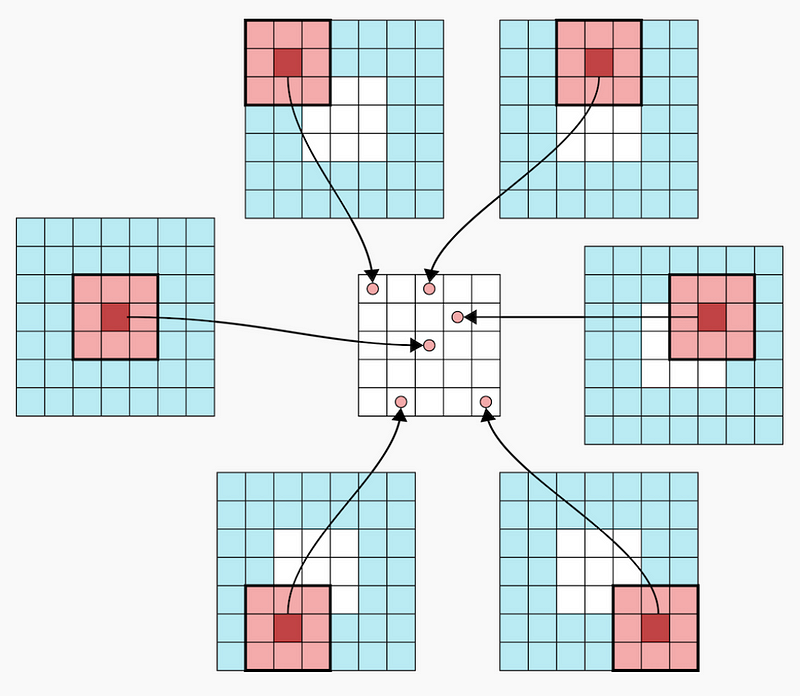
当在Keras中使用时，例如在变分自动编码器的开发中，这些是使用upsampling层实现的。
原文地址：https://towardsdatascience.com/advanced-topics-in-deep-convolutional-neural-networks-71ef1190522d
