深度学习之Attention机制
Encoder-Decoder的深度学习架构是目前非常流行的神经网络架构,在许多的任务上都取得了很好的成绩。在之前的博客中,我们也详细介绍了该架构(参见深度学习之Encoder-Decoder架构)。本篇博客将详细讲述Attention机制。来自如下论文:
加载中...
Encoder-Decoder的深度学习架构是目前非常流行的神经网络架构,在许多的任务上都取得了很好的成绩。在之前的博客中,我们也详细介绍了该架构(参见深度学习之Encoder-Decoder架构)。本篇博客将详细讲述Attention机制。来自如下论文:
欢迎关注 DataLearner 官方微信,获得最新 AI 技术推送

Encoder-Decoder结构使用一个encoder网络和一个decoder网络来建模。Encoder神经网络读取数据,并将其转换成一个固定长度的向量。而Decoder网络则从Encoder的输出向量开始,将其转换成目标向量。这两个部分的网络共同训练最终最大化给定原数据条件下,目标序列的概率。
但是这个结构有一些问题。首先,它必须要把所有的原始数据压缩成一个固定长度的向量来表示。这对于处理很长的句子很困难。因为太长的句子压缩之后可能会丢失句子靠前的信息。随着序列的增长,基础的Encoder-Decoder模型的性能会显著下降。
为了解决上述问题,研究者提出了Attention机制。这是Encoder-Decoder架构中很重要的机制,它显著提升了Seq2Seq模型的效果。和原始的Encoder-Decoder架构相比,该模型提出了使用情景向量,即context vector来编码指定位置的原始序列信息,帮助Decoder阶段的解码过程。在Decoder的模型中,context vecotr与上阶段的输出信息一起别用来预测目标序列的结果。与原始Encoder-Decoder架构最大的不同就是,Attention不再将一整个句子进行编码,而是在预测不同位置的序列的时候使用不同的原始信息。
原始的RNN Encoder-Decoder模型是将一个向量序列$\bold{x}=(x_1,\cdots,x_{T_x})$转换成一个中间向量$c$。其中Encoder阶段中每一个单元的处理如下:
h_t = f(x_t,h_{t-1})
也就是每个单元通过一个处理,将上一阶段的状态变量$h_{t-1}$和该阶段的数据$x_t$一起转换成本阶段的状态变量(GRU和LSTM形式类似,只是内部多了一些门来处理状态变量,LSTM多了一个状态变量。可参考GRU深度学习网络和LSTM网络)。
最后,输出的变量为:
c = q(\{h_1,\cdots,h_{T_x}\})
这里的$f$和$q$都是非线性变化,中间变量是将所有的状态变量合到一起做了一个转换。在Decoder阶段,主要计算的是如下的联合概率:
p(\bold{y}) = \prod_{t=1}^T p(y_t|y_1,\cdots,y_{t-1}, c)
其中,$\bold{y}=(y_1,\cdots,y_{T_y})$。在RNN中,每一个条件概率的建模如下:
p(y_t|y_1,\cdots,y_{t-1}, c) = g(y_{t-1}, s_t,c)
其中,$g$是非线性变化,可以是一个多层的网络,目的是输出$y_t$,$s_t$是RNN的隐状态,是Decoder阶段的隐状态。
Attention机制中,Decoder阶段的序列预测不再仅仅依赖上一阶段的状态变量$s_{t-1}$,上一阶段的序列预测$y_{t-1}$和Encoder阶段的输出向量$c$,而是对不同的输出位置的标签,使用不同的情景向量$c_i$。如下图所示:
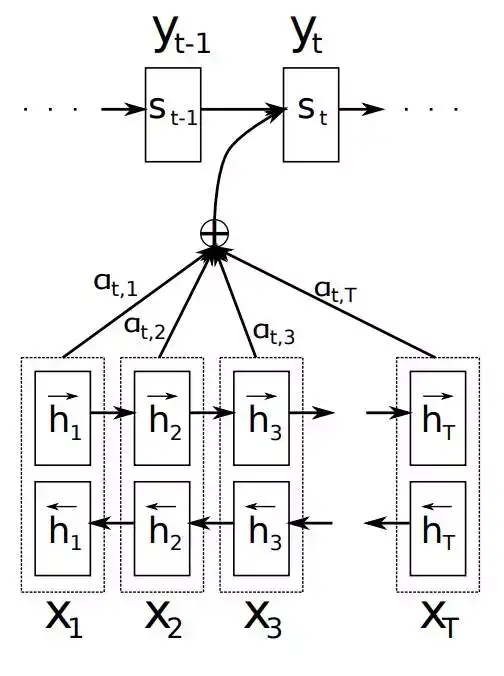
在Attention机制中,Decoder阶段的条件概率如下:
p(y_t|y_1,\cdots,y_{t-1}, \bold{x}) = g(y_{t-1}, s_t,c_i)
注意,原始的Encoder-Decoder,该阶段的条件概率的条件是Decoder前面的状态和Encoder的输出向量$c$,而Attention机制中,这里的条件概率的条件是Decoder前面的状态$y_1,\cdots,y_{t-1}$和原始的数据$\bold{x}$。上述$s_{t}$依然是Decoder阶段的状态变量,其计算如下:
s_t = f(s_{t-1}, y_{t-1}, c_i)
这里的$c_i$是与每一个预测标签$y_i$相关的情景向量。它依赖于输入数据的输出状态序列$(h_1,\cdots,h_{T_x})$。每一个标注$h_i$都是整个序列中输出数据最关注的哪一部分。后面我们再来描述它。
情景向量$c_i$的计算如下,它是输入数据状态的加权求和结果:
c_i = \sum_{j=1}^{T_x}\alpha_{ij}h_j
这里的权重计算如下:
\alpha_{ij} = \frac{\exp (e_{ij})}{ \sum_{k=1}^{T_x}\exp (e_{ik})}
其中,
e_{ij} = a(s_{i-1}, h_j)
它的含义是定义输入数据的位置$j$与输出序列位置$i$的远近程度(或者说是匹配程度,有时候不一定位置一样就能匹配)。因此,这里的含义就是,如果输入数据的位置与当前输出的位置越匹配,那么它的状态变量就影响越大。它是由Decoder前一个阶段的状态变量和输入数据的第$j$个阶段的状态变量决定。而其系数$a$则是一个参数,通过学习得到。
可以这样理解,设$\alpha_{ij}$是目标数据$y_i$来自原始输入数据$x_j$的状态的概率。那么,第$i$个情景向量$c_i$是所有可能的输入序列的概率之和了。
我们换个角度去理解,原来的非Attention机制下,Decoder阶段的RNN(GRU和LSTM都是类似)每个CELL的输入是前一阶段的状态$s_{t-1}$和本阶段的数据输入$y_{t-1}$(因为Encoder-Decoder架构中Decoder阶段的每一个CELL的数据输入是前一阶段的实际标签)。而加了Attention机制之后,这里每个CELL的数据输入变成了attention vector。
我们以吴恩达课程的联系作业图片为例:

这个Attention模型中的Encoder阶段是一个Bi-LSTM(称为Pre-attention Bi-LSTM),Decoder阶段的模型师LSTM(称为Post-attention LSTM)。在计算了Encoder阶段之后,Encoder阶段产生了组隐状态:
a^{< i>} = \begin{bmatrix}
a^{< i>\leftarrow} \\
a^{< i>\to}
\end{bmatrix}
这里的箭头方向表示Bi-LSTM两个不同方向产生的隐状态。接下来,这些Encoder阶段产生的状态变量将与Decoder阶段的状态变量一起产生attention权重,并最后产生attention向量。具体的过程如下图所示:
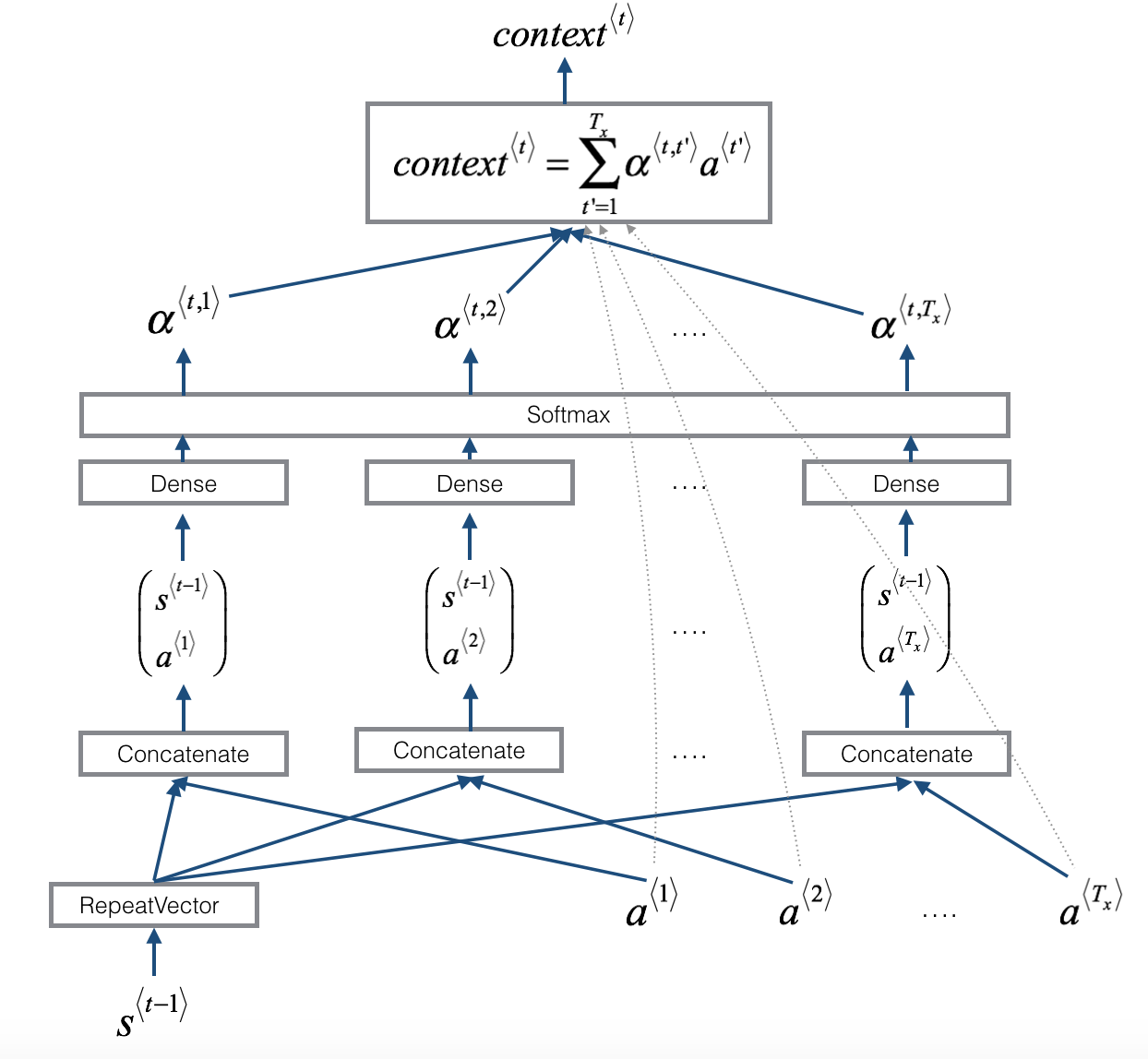
注意到,上面产生Attention向量的过程也可以理解为一个小型的神经网络,所以这里产生attention向量的方式与一个神经网络是类似的。在这个过程中,首先用Decoder上一阶段的状态变量$s_{t-1}$和所有的Encoder阶段的状态变量一起组成一个新的矩阵:
\begin{bmatrix}
s^{< t-1>} \\
a^{< i>}
\end{bmatrix}
这个向量需要通过一个全连接的网络(Dense)产生中间变量$e_{ij}$,这就是上述公式的最后一个:
e_{ij} = a(s_{i-1}, h_j)
接下来,我们注意到attention权重的计算其实是一个softmax的激活函数(这里的$\alpha_{ij}$就是图中的$\alpha^{< t,1>}$等的变量):
\alpha_{ij} = \frac{\exp (e_{ij})}{ \sum_{k=1}^{T_x}\exp (e_{ik})}
接下来我们就可以通过这个attention权重系数和Encoder阶段的状态变量$h_j$(这里公式的$h_j$就是图中的$a^{< 1>}$之类的变量)一起产生最终的context向量(attention向量):
c_i = \sum_{j=1}^{T_x}\alpha_{ij}h_j
最终,这个变量和上一个阶段的状态变量输出一起,作为本阶段CELL的输入计算即可。这样就是Decoder阶段完整的CELL计算过程。其中Attention的代码如下:
# Defined shared layers as global variables
repeator = RepeatVector(Tx) #<Gema> Repeats the input Tx times.
concatenator = Concatenate(axis=-1) #<Gema> Layer that concatenates a list of inputs. axis: Axis along which to concatenate, in this case, on the last axis.
densor1 = Dense(10, activation = "tanh") #<Gema> Just your regular densely-connected NN layer.
#<Gema> Dense implements the operation: output = activation(dot(input, kernel) + bias) where kernel is a weights matrix created by the layer
densor2 = Dense(1, activation = "relu")
activator = Activation(softmax, name='attention_weights') # We are using a custom softmax(axis = 1) loaded in this notebook
#<Gema> Applies an activation function to an output.
dotor = Dot(axes = 1)
#<Gema> Layer that computes a dot product between samples in two tensors.
def one_step_attention(a, s_prev):
"""
Performs one step of attention: Outputs a context vector computed as a dot product of the attention weights
"alphas" and the hidden states "a" of the Bi-LSTM.
Arguments:
a -- hidden state output of the Bi-LSTM, numpy-array of shape (m, Tx, 2*n_a)
s_prev -- previous hidden state of the (post-attention) LSTM, numpy-array of shape (m, n_s)
Returns:
context -- context vector, input of the next (post-attetion) LSTM cell
"""
### START CODE HERE ###
# Use repeator to repeat s_prev to be of shape (m, Tx, n_s) so that you can concatenate it with all hidden states "a" (≈ 1 line)
s_prev = repeator(s_prev)
# Use concatenator to concatenate a and s_prev on the last axis (≈ 1 line)
concat = concatenator([a,s_prev])
# Use densor1 to propagate concat through a small fully-connected neural network to compute the "intermediate energies" variable e. (≈1 lines)
e = densor1(concat)
# Use densor2 to propagate e through a small fully-connected neural network to compute the "energies" variable energies. (≈1 lines)
energies = densor2(e)
# Use "activator" on "energies" to compute the attention weights "alphas" (≈ 1 line)
alphas = activator(energies)
context = dotor([alphas,a])
context